Найдите наименьшее значение функции f(x)=x+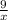 на интервале (0; ∞)
на интервале (0; ∞)
Другие вопросы по теме Математика
Популярные вопросы
- Найти диагонали равнобедренной трапеции основания которой равны...
3 - Решити по матиматике у маши была 40 карандашей а у ирины 39 а у...
3 - Напишите каноническое уравнение эллипса, если даны его полуоси...
3 - Решите уравнения! х(240: 2)=15, с-130*50=0 ,х: (240: 2)=1...
1 - Зточки кола проведено 2 хорди що доривнюють радиусу . знайдить...
2 - Во время экспедиций -вокруг экспедиций перестройте простые предложения...
3 - Ящик тянут по земле за веревку по горизонтальной окружности длиной...
2 - Напишитесостав слов ручка, круча и ручной....
2 - 921-(506-+428) последовательность решения...
3 - Зделать ластівка першого дня пролетіла 3км 578м, а другого дня-...
3
Пошаговое объяснение:
x₁=3 x₂=-3 ∉(0;+∞).
ответ: унаим=6.