Найдите наибольшее значение функции z = 8 + 4x – 3y в замкнутой области G : x2 + y2 ≤ 4
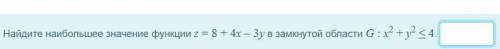
Другие вопросы по теме Математика
Популярные вопросы
- Мини -очинение на тему мой день рождения...
1 - Подготовьтесь записать предложения. город встречает рассвет. лучи солнца...
3 - 1)население и хозяйство страны в 16 веке.2) православная церковь в 17...
3 - Визначте, скільки витрачено електроенергії на рафінування 5 т міді ,...
2 - Биологическая .насколько справедливо с биологической точки зрения выражает...
2 - Для сжигания навески смеси серы и угля массой 25 г потребовался кислород...
1 - Ко всем относится. в треугольнике авс угол с = 90 градусов: 1. ас =...
1 - Нужен реферат на тему экологические проблемы растениеводства и животноводства...
3 - 8/9+2/3*1,7. , решить. сижу туплю....
2 - Новруз — в азербайджане называют новруз байрамы. наряду с новым годом...
1
ответ: 18
Пошаговое объяснение:
Решаю без нахождения частных производных и функции Лагранжа и без геометрического пересечения плоскости с цилиндром.
z=8+4*x-3*y
Пусть :
x^2+y^2 = a^2 <=4 ( -2<=a<=2 )
Откуда можно считать , что
x= a*cos(t)
y=a*sin(t)
z= 8+ a*(4*cos(t) -3*sin(t) )
Используя метод вс аргумента , очевидно что :
4*cos(t) -3*sin(t) = √(3^2+4^2) * sin(Ф) = 5*sin(Ф)
-5<=5*sin(Ф)<=5
Очевидно , что z принимает наибольшее значение , когда
a и 4*cos(t) -3*sin(t) максимальны по модулю и имеют одинаковый знак , таким образом
zmax = 8+2*5 =18