Найдите наибольшее значение функции y=(x+8)^2(x+1)−3 на отрезке [− 15 ; − 7].
Ответы
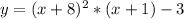
![[-15;-7]](/tpl/images/0734/1767/07b33.png)
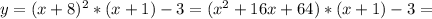
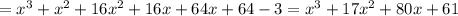
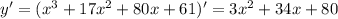
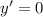
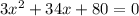
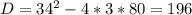
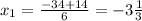 ∉
∉ ![[-15;-7]](/tpl/images/0734/1767/07b33.png)
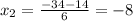 ∈
∈ ![[-15;-7]](/tpl/images/0734/1767/07b33.png)

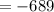 - наименьшее
- наименьшее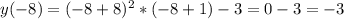 - наибольшее
- наибольшее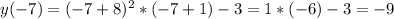
Другие вопросы по теме Математика
Популярные вопросы
- Вспомните какие рассказы л.н толстого вы изучали.запишите художествиные...
1 - Если на страницу помещается 32 строки то весь текст займёт 52 листа....
1 - Как сказочный часовой, уселся на голой ветке головастый серый совёнок....
3 - Вмагазин 5 ящиков с марковю а со свёклой 2 ящика меньше.сколько ящиков...
2 - Периметр прямоугольника 30 см. найдите его стороны, если известно...
3 - Сравните числа: 5/5и1; 7/6и1; 16/17и1...
1 - От двух пристаней растояние между которыми 120 км скорость одного...
1 - Сколько шестых долей единицы содержится: в 3 единицах и в 12 единицах?...
2 - Реши следующую разными три грузовика перевезли 24 т груза. сколько...
3 - От двух станций одновремено навстречудруг другу отправились два поезда...
2