Найдите наибольшее значение функции
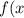 = 5 - 2 sin^{4}(x) - 2 \cos^{4} (x))
Другие вопросы по теме Математика
Популярные вопросы
- Замени сочетание имён существительных с прилогательными сочетаниями глаголов...
1 - Какое спряжение у слов отражаются похож и скрываются...
3 - Как решить примеры: 8 дм2 2 см2-58 см2 96 мм2 38 а 54 м2 * 7 80 м2 72...
3 - Составить 10 предложений на тему: обособление определений...
1 - Translate into english (переведите только правильно! ) 1)не хотите схъодить...
1 - Напишите 5 наречий от слова рассказывать....
1 - ответьте на вопросы (про себя) что то типа сочинения! по 2-4 предложения...
2 - На примерах слов (пила-пила,стекло-стекло,дали -дали,дуло-дуло,жгут-жгут)показать,как...
1 - Запорожская сечь.что она из себя представляла? каковы законы и порядки?...
3 - Сократите дробь и запишите результат в виде смешенной дроби 10\4 30\20...
2
4
Пошаговое объяснение:
f(x)=5-2·sin⁴x-2·cos⁴x=5-2·(sin⁴x+cos⁴x)=
=5-2·(sin⁴x+2·sin²x·cos²x+cos⁴x-2·sin²x·cos²x)=
=5-2·(sin⁴x+2·sin²x·cos²x+cos⁴x)+4·sin²x·cos²x=
=5-2·(sin²x+cos²x)²+sin²2x=5-2·1²+sin²2x=5-2+sin²2x=3+sin²2x
Так как наибольшее значение функции sin²2x равно 1, то наибольшее значение функции f(x)=3+sin²2x равно 3+1=4.