Найдите наибольшее и наименьшее значение функции 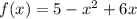
заданной на отрезке [1;4]
![Найдите наибольшее и наименьшее значение функции заданной на отрезке [1;4]](/tpl/images/3776/3607/89048.jpg)
Другие вопросы по теме Математика
Популярные вопросы
- первый вариант начертите координатный луч за единицей отрезка введите отрезок длиной...
2 - Лабораторная работа 1 определение ускорения тела при равноускоренном движении...
3 - Как возраст влияет на социальное положение в обществе...
3 - Провідник завдовжки 50 см завис в однорідному магнітному полі перпен дикулярно до...
1 - Охарактеризувати рух тіла за поданим графіком...
1 - ПРИДУМАТЬ сказку об экологии для детей (за копирование жалоба)...
1 - 7. Площа парти 0,9 м2. Виразіть цю площу у квадратних сантиметрах....
1 - Доказать, что число16^20+2^76 делится на 17С подробным объяснением!...
2 - Здравствуйте . На диаграмме показано содержание питательных веществ в сухарях *к...
2 - В одном из приведённых ниже предложений НЕВЕРНО употреблено выделенное слово. Исправьте...
1
Пошаговое объяснение:
f(x) = 5-x² +6x на отрезке [1;4]
посмотрим, есть ли точки экстремума у этой функции на заданном отрезке
f'(x) = 0 - это необходимое условие экстремума функции
f'(x) = (5)' - (x²)' + (6x)' = 6-2x = 2(3-x) ⇒ x = 3 - критическая точка и попадает в наш отрезок
теперь ищем значение функции на концах отрезка и в критической точке
f(3) = 14 - максимум в т х = 3
f(1) = 10 - минимум в т х=1
f(4) = 13