1. Математика
  2. Найдите наибольшее целое

Найдите наибольшее целое значение параметра P , при котором заданное неравенство выполняется при всех значениях x: x2+4(z+p)>p^2


Найдите наибольшее целое значение параметра P , при котором заданное неравенство выполняется при вс

loloh333 loloh333    2   17.07.2020 11:19    2

Ответы
anna2016anna20 anna2016anna20  15.10.2020 15:25

2

Пошаговое объяснение:

Если неравенство выполняется для всех значений x, то оно выполняется и для x=1-p: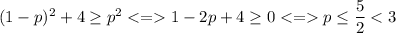 (1-p)^2+4\geq p^2 1-2p+4\geq 0 p\leq \dfrac{5}{2} Тогда максимально возможное целое значение, которое может принимать p, равно 2. Проверим, удовлетворяет ли оно условию.

x^2+4|x+2|\geq 4\\ \left[1\right]\;x\geq -2:\;x^2+4x+8\geq 4x^2+4x+4\geq 0(x+2)^2\geq 0x\in R\\ =x\geq -2\\ \left[2\right]\; xx+2x-6\leq 0=x\leq 6\\ =x< -2\\ \left[\begin{array}{c}x\geq -2\\xx\in R

- Верно.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Волковаксюша Волковаксюша  20.08.2019 01:00
Объясните, от чего зависит величина припуска на обработку?...
Флаксария Флаксария  20.08.2019 01:00
Какая из кошек,белая или чёрная,раньше разбудит собаку? на сколько минут раньше? белая-скорость=3,8 км.ч чёрная=3.5 км.ч белой осталось дойти=380м а чёрной=175м....
skZ1 skZ1  20.08.2019 01:00
Для подъема на гору потребовалось 2ч 45 мин., а для спуска с нее 1ч 35 мин., сколько всего времени потрачено на подъем и спуск?...
Masha200605 Masha200605  20.08.2019 00:50
Впачке 14 листов картона и 12 листов бумаги. из пачки взяли 6 листов на урок технологии.сколько листов осталось в пачке?...
89286666666 89286666666  20.08.2019 00:50
Реши уравнения 3класс 350÷а=50,300÷а=50,х÷5=70,х÷5=60....
AndruxaS AndruxaS  20.08.2019 00:50
Подскажите хотя бы один пример, ! придумай приклади на додавання з переходом на это как?...
sweetcarpet258 sweetcarpet258  20.08.2019 00:50
Кто смотрел фильм александр невский ? если кто нибудь смотрел,то ответьте на вопросы: главный герой фильма? где проходила битва? кто и почему победил в битве ? как музыка...
ARTEMONUM ARTEMONUM  20.08.2019 00:50
Как решить. 128-7×4+22, 192+36: 9-14, 335-9×5+67,, 25+88-7×5...
kril20101 kril20101  20.08.2019 00:50
Еше два примера найти знач произ 5\11*22\25 8\35*5\12...
alihannurmambe alihannurmambe  20.08.2019 00:50
Отметь разности которые ты можешь вычислить пользуясь равенствами 6+2=8 и 3+4=7 и запиши их...

Популярные вопросы