Найдите наибольшее целое решение неравенства: (x-2)^2(x+4)^3/x+7 меньше или равно 0
Можно пошаговое решение
Другие вопросы по теме Математика
Популярные вопросы
- Расскажите подробно путь митраши из произведения кладовая солнца...
2 - No2,caso4, baoh2, so2, mnoh2, hno3, nacl,fe2(so4)3, cao,kno3, mgo, fe2o3, na2so4,...
2 - 2x-1/4-x+3/8 -4 решите неравенство,...
1 - Подскажите как зовут лисичку- из enjoy english?...
1 - Переведите с не с переводчика) 1. où et quand julie et ses copains se sont-ils retrouvés?...
2 - Перевод ! (не через ! ) потребление электроэнергии неблагоприятно сказывается на...
2 - Скласти 6 речень росповідне,питальне,та спонукальне про 8 березня...
3 - Всё про любое произведение из страсти по матфею и.с.бах...
1 - Вычисли в столбик 436+564= 76+924= 1000-481=...
1 - Са)кролик вырастил на грядке 48 морковок,что составило 4/7 от того количества,о...
3
Відповідь:
х є (-7 ; -4] ∪ {2}
Покрокове пояснення:
Для того что бы решить данное неравенство, из вида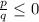 превратим в вид
превратим в вид 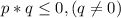
(х-2)²(х+4)³(х+7)≤0 (х+7)≠0
Для того, что бы решить такое неравенство, нужно сначала решить уравнение, и найти промежутки:
(х-2)²(х+4)³(х+7)=0
(х-2)=0 (х+4)=0 (х+7)≠0
х=2 х=-4 х≠-7
Три точки делают 4 промежутка, проверим каждый из них:
1) Из промежутка (-∞ ; -7) возьмем число -10
Неверно, так как минус на минус даст плюс, число > 0
2) Из промежутка (-7 ; -4) возьмем число -5
3) Из промежутка (-4 ; 2) возьмем число 0
4) Из промежутка (2 ; +∞) возьмем число 3
Тогда нам подойдет только промежуток (-7 ; -4) и 2 числа, 4 и 2, тогда ответ будет таким: х є (-7 ; -4] ∪ {2}