Найдите наибольшее целое решение неравенства? Если можно с подробным решением.

Другие вопросы по теме Математика
Популярные вопросы
- Получите выражение для потенциальной энергии материальной точки массой...
3 - Алгебра нужны ответы кто решит?...
2 - Оформите свое решение и напишите ответ.Извините за качество....
3 - Решить систему уравнений 2(5а-4)-3(3-4в)=5 6(7в-1)-(2+3а)=31...
1 - Які природоохоронні об єкти є в Миколаївській област...
1 - ЗАДАНИЯ:1. Налоговый инспектор составил протокол об административном правонарушении...
2 - На стороне AB прямоугольника ABCD как на диаметре построена окружность...
1 - 10. Отметь знаком все слова,которые при раскрытии скобокпишутся раздельно.о...
1 - Преобразовать прямую речь в косвенную. Врач согласился: У вас все хорошо...
2 - До кола з центром O проведенну дотичну AB ( B - точка дотику ) Знайдіть...
1
4
Пошаговое объяснение:
Пусть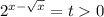
Наибольшее целое решение — x = 4.