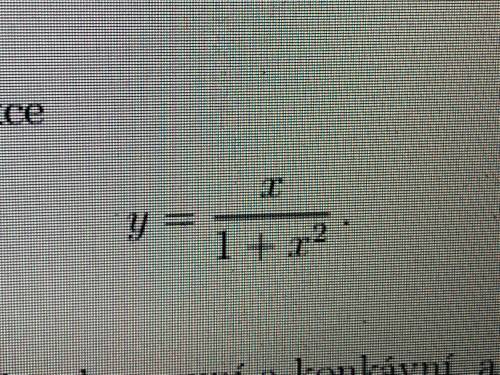
Математика: Найдите локальный экстремум функции

Найдите локальный экстремум функции

Ответы

ЕваКимСокДжин 04.02.2021 13:20

Пошаговое объяснение:

вообще-то, если локальный, то на отрезке

ну да ладно

$y=\frac{x}{1+x^2}$

производная функции

$y'=\frac{x'(1+x^2)-x(1+x^2)'}{(1+x^2)^2} = \frac{1-x^2}{(1+x)^2}$

$\frac{1-x^2}{(1+x)^2} =0;$ ⇒ x₁ = -1; x₂ = 1; - это критические точки

используем достаточное условие экстремума функции одной переменной. найдем вторую производную:

$y''=\frac{1-x^2}{(1+x^2)^2} =\left[\begin{array}{ccc}( \frac{u}{v})' =\frac{u'v-uv'}{v^2} \\\\\end{array}\right] = \frac{2x(x^2-3)}{(x^2+1)^3}$

вычислим значение второй производной в критических точках

y'' (-1) = 1/2 > 0 - значит х₁= -1 это точка минимума и у(-1) = -1/2

y''(1) = -1/2 < 0 -значит х₂= 1 это точка максимума и у(1) = 1/2

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

kairat0101 20.06.2019 19:20

adilymnuk 20.06.2019 19:20

0Frozen0 20.06.2019 19:20

evelina2023 20.06.2019 19:20

iamash2450 20.06.2019 19:20

naoimiiwsvb2 20.06.2019 19:20

KrystallBlack 20.06.2019 19:20

PsyhovanayaPechenka 20.06.2019 19:20

vipsab333 20.06.2019 19:20

оалклклкл 20.06.2019 19:20

Найдите значение: m, если -m = 2/3...