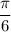Найдите корни уравнения 2 sin2 (3π / 2 – x) + 5 sin x = 4 на промежутке [0; π / 2].
Другие вопросы по теме Математика
Популярные вопросы
- Өздік, белгісіздік, сұрау есімдктермен сөйлем құрастыр. что это значит скажите...
2 - Составьте тестовое задание с выбором трех правильных ответов из шести, к котором...
1 - 1)a²-b²-(a-b) 2)p²-b-p-b² 3) 16•3-25y² 4)100m²-10m+9n-81n² решыть роскласты на...
3 - Та атомамиа влау, азчинkоосchocyk:) HanuvimoалканиTakitкесекmaCanoerlundMetan...
1 - Кароче просто ответь.ты тупой если тупой ответь ...
3 - синтаксический разбор предложения: Земля стала похожа на гаммах подвешенный над...
2 - Решите задачу. Масса пачки печенье 125г,а масса пачки сухарей 380 г. Что тяжилей....
3 - ПЛЮСЫ И МИНУСЫ ДВОРЯНСКОЙ ЖИЗНИ...
3 - Выпишите выделеные местоименя опредилите их разряд и форму укажите особенности...
2 - УС Прочитайте 2 часть повести ТриКе, в которой Алиса, алтан у отмиелофон, отправляется...
2
Синус ограничен: [-1;1]. Поэтому первое выражение не имеет решений.
В заданном промежутке присутствует только один корень: