Найдите количество натуральных значений , которые может принимать функция y=-3,2*sin(x-п/12)
Другие вопросы по теме Математика
Популярные вопросы
- Смешали 40%-й раствор кислоты с 15%-м раствором и получили 1400...
3 - В школьном кабинете химии имеется V0=1500 см3 раствора кислоты,...
2 - Установите соответствие между функциями обществознания. 1) Разработка...
2 - Из приведённых ниже тел выбери и отметь те, колебания которых...
3 - Таңырыптың біреуін таңдап 10-15 сөйлем жазаңыз. Мән көрмесінде....
2 - Гражданин РФ в 1995 году выехал за пределы РФ и остался постоянно...
2 - 2. Выразите переменную а через переменную в в выражении: (3a...
2 - не пишите фигню, реально нужно...
3 - Система планирования потребности в материальных ресурсах должна...
3 - Придумайте , напишите 24 реплики диалога разговаривающих 2 человека...
1
Множеством значений функции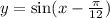 является отрезок
является отрезок ![[-1;1].](/tpl/images/1359/9273/1bbb2.png) Эту функцию можно записывать в виде двойного неравенства.
Эту функцию можно записывать в виде двойного неравенства.
Умножим все части неравенства на число (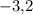 ), учитывая смены знаков неравенства.
), учитывая смены знаков неравенства.
Функция может принимать значения![[-3{,}2;3{,}2]](/tpl/images/1359/9273/67133.png) из них
из них 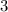 натуральных значений.
натуральных значений.
ответ: ответ: 3
Пошаговое объяснение:
y=-3,2*sin(x-п/12)
-1≤sin(x-п/12) ≤1умножим на -3,2
-3,2≤sin(x-п/12) ≤3,2
Между числами -3,2 и 3,3 находются следующие натуральные числа: 1,2,3 их всего 3
ответ: 3