Найдите функцию f(x) для которойF(x)=tg4x является первообразной на 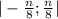
Другие вопросы по теме Математика
Популярные вопросы
- Разобрать по составу слова ворон, ворона, воронье, по вороньему, проворонят....
1 - Напишите план текста студент (чехов)...
2 - Отрезок ef равен 17/20 m, и он длиннее отрезка ak на 5/8 м. найдите длину отрезкаak....
2 - Устав после уроков ,мне не работалось. осажденный бросали со стен крепости камни...
2 - Периметр прямоугольника abcd равен 0,8м, стороны относятся как 1 к 0,6. найди...
2 - Римская цифра если младшая цифра стоит справа от старшей, то ее нужно...
2 - Найти площадь боковой поверхности правильной четырехугольной пирамиды угол пирамиды...
1 - Расспредели слова по группам в зависемости от орфограммы. запиши. аллея, окрестность,...
3 - Много тому,кто найдет сложную производную этих двух примеров,что во вложении...
1 - Что такое орфограмма? список орфограмм....
1
Для этого, мы можем воспользоваться формулой интегрирования для функции тангенса:
∫ tan(x) dx = ln|sec(x)| + C, где C - постоянная интегрирования.
Используя эту формулу, мы можем интегрировать функцию F(x) = tan(4x):
∫ tan(4x) dx = 1/4 * ∫ tan(u) du, где u = 4x.
Заменяем переменную, получаем:
1/4 * ∫ tan(u) du = 1/4 * ln|sec(u)| + C.
Теперь, чтобы найти f(x), нам нужно заменить переменную обратно:
f(x) = 1/4 * ln|sec(4x)| + C.
Таким образом, функция f(x), для которой F(x) = tan(4x) является первообразной на (| -n/8, n/8 |), где n - произвольное положительное число, равна f(x) = 1/4 * ln|sec(4x)| + C, где C - произвольная постоянная интегрирования.