Найдите действительные значения x,при которых функции f: r-r,f(x)=-(x-4)^2, и g: r*-r*,g(x)=4/x,убывают. обоснуйте ответ!
Другие вопросы по теме Математика
Популярные вопросы
- Длина зала аэровокзала - 150м,а ширина 80м.полы зала ожидания выложены мраморной...
3 - Написать 5-6 предложений и + обозначить части речи...
2 - Как решить подробно это уравнение 3,35+6,8у-2,3у+5,8=18,6...
3 - Сочинение не большое про частную и государственную школу(отдельно)на . языке,...
2 - Составте предложения со словами to pass, to kill, a fire, a life, to carry...
1 - Диалог на о покупке любого вида одежды...
1 - Культура народов мира в новом времени! надо!...
3 - Сочинение-миниатюра« если бы я был директором кондитерской фабрики»...
3 - Разложите не множители (y-3)в кубе+(y+1)в кубе...
2 - Іть будь ласка , треба скласти словниковий диктант с -ри ,ли, ере,еле...
2
Производная отрицательна на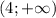 , значит функция убывает на этом промежутке.
, значит функция убывает на этом промежутке.
Производная отрицательна на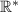 , значит функция убывает на всей области определения.
, значит функция убывает на всей области определения.