1. Математика
  2. Найдите число пар (x , y )

Найдите число пар (x , y ) которые принимают целые значения Удовлетворяющих уравнению


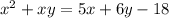
x^2+xy=5x+6y-18

paniann17 paniann17    1   05.12.2021 11:02    0

Ответы
ОлесяБычкова ОлесяБычкова  20.01.2022 05:27

x^2+xy=5x+6y-18

Выразим y из уравнения:

x^2-5x+18=6y-xy

x^2-5x+18=(6-x)y

y=\dfrac{x^2-5x+18}{6-x}

Выделим целую часть в получившейся дроби:

\dfrac{x^2-5x+18}{6-x}=-\dfrac{x^2-5x+18}{x-6}=-\dfrac{x^2-6x+x-6+6+18}{x-6}=

=-\dfrac{x(x-6)+(x-6)+24}{x-6}=-\dfrac{(x-6)(x+1)+24}{x-6}=

=-\left(x+1+\dfrac{24}{x-6}\right)=-x-1-\dfrac{24}{x-6}

Таким образом:

y=-x-1-\dfrac{24}{x-6}

То есть, если выражение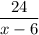 \dfrac{24}{x-6} является целым, то тогда значение y также будет целым.

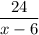Остается выяснить, при каких целых x выражение \dfrac{24}{x-6} является целым (точнее, сколько таких x).

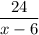Если (x-6) является делителем числа 24, то дробь \dfrac{24}{x-6} представляет собой целое число.

Перечислим целые делители числа 24:

\pm1;\ \pm2;\ \pm3;\ \pm4;\ \pm6;\ \pm8;\ \pm12;\ \pm24

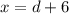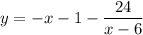Имеется 16 целых делителей у числа 24. По каждому делителю d можно будет найти целое значение x=d+6, а по каждому значению x можно будет найти значение y=-x-1-\dfrac{24}{x-6}.

ответ: 16 пар

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
seropyan2006 seropyan2006  08.06.2019 05:00
Магазин продал 784 кг. яблок,груш и слив.яблок было продано в 3 раза больше ,чем груш,а сливы составляли 5\28 всех проданных фруктов.сколько магазин выручил денег за проданные...
Kepka229 Kepka229  08.06.2019 05:00
4портнихи за 5 дней сшили 140 костюмов сколько костюмов сошьют 11 портних за 3 недели...
matveydayp0cd3p matveydayp0cd3p  08.06.2019 05:00
Вкоробку с синими какандашами сначала положили 11 красных карандашей, а затем половину всех карандашей переложили в пенал. после этого в коробке осталось 16 карандашей. сколько...
taric2004 taric2004  08.06.2019 05:00
Сколько осей симметрии имеет пятиконечная звезда?...
lilyok2006 lilyok2006  08.06.2019 05:00
Для школы купили несколько линеек по 3 руб. и столько же карандашей по 2 руб. за линейки заплатили 30 руб. сколько денег заплатили за карандаши?...
raisara raisara  08.06.2019 05:00
Как начертить угол абдкоторый равен75градусов...
МихаилШуршалов МихаилШуршалов  08.06.2019 05:00
1)сколько магазин продал яблок и груш? сколько было продано слив? сколько продано яблок? сколько продано груш? 2)расположи вопросы в порядке убывания кол-ва действий сама : магазин...
halker249Neekolay halker249Neekolay  08.06.2019 05:00
Вкаком году был установлен,и каким событиям посвящен памятник минину и ?...
koksenenko10 koksenenko10  08.06.2019 05:00
Объясни, зачем современному человечеству такая международная организация оон...
НяхаВай НяхаВай  08.06.2019 05:00
Во франции путешественники несколько килограммов яблок по 9 франков, и столько же килограммов апельсинов по 6 франков. за апельсины заплатили 18 франков. сколько денег заплатили...

Популярные вопросы