Найдите частные решения дифференциальных уравнений.
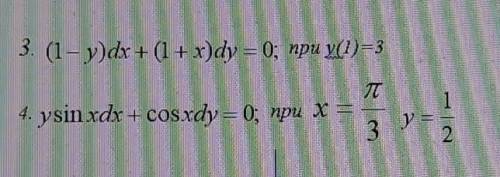
Другие вопросы по теме Математика
Популярные вопросы
- Надеюсь вам видно если даже не видно попытайтесь решить мне очень...
3 - Задание 3. Из последнего абзаца выпишите все союзы, которые есть....
3 - Background (bg)- задает название для кнопки определяет фон объекта...
2 - Сын есімдерді тауып, олардың дара немесе күрделі екенінайт.пі...
2 - Мировой экономический кризис На какие сферы экономики повлияла...
2 - Якої довжини треба взяти ніхромовий дріт із площею поперечного...
1 - 3 Faites des phrases. 1)Aziz2)vaa l école à Samarkanden Francechez...
3 - Deutsch! Deutsch! Deutsch! Напишите , любовную история, около...
2 - Розобрать слова :хлібопіч,передвесняний ,покупець,учителька ,прекрасний,прибавити,водянистий,ліс,щоденник,міський....
3 - Решите 1,25-4 1/12;-2 1/8-3,4;5•(-2/3)+1,8;4,5•(-5 1/3)•(-0,125);15:(-5/7)-2...
1
общее решение
частное решение
общее решение
частное решение