Найдите 9-ю производную функции f в точке x=0
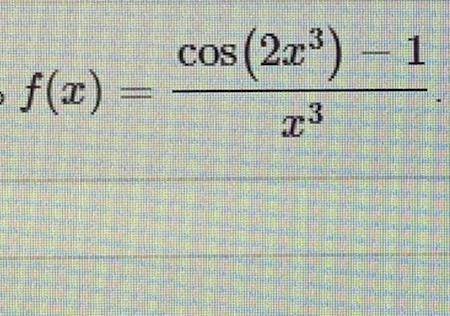
Другие вопросы по теме Математика
Популярные вопросы
- Скоротіть дріб очень нужно ...
2 - . 1С каких земель в Индии налог не взимался? А – икта В – халиса С - вакуфные...
3 - Кардинальна зміна життя християнина виявляється перш за все у... (закінчіть...
3 - Найти интервалы монотонности функции. Фото....
1 - тема: проблемы семьи в древнем мире и в наше время реферат кратко...
3 - Як кожен із творів висвітлює причини Національно-визвольної війни? Чому...
3 - Aufgabe 1 Arbeitszeit: 20 Minuten Schreiben Sie eine E-Mail (circa 80 Wörter)....
2 - (если можно вышлите ответ фотографию ответа)...
3 - До іть . З одного міста в друге , відстань між якими 240 Км,виїхали одночасно...
2 - Could: Form polite questions. e.g. Could you remember me to ypur parents,...
2
Предоставленный график функции f(x) показывает, что функция f(x) состоит из сегментов прямых линий. Каждый сегмент может быть описан линейной функцией вида y = mx + c, где m - наклон прямой, а c - точка пересечения с осью ординат.
По графику видно, что у функции f(x) три разных сегмента:
- Для x < -1, функция f(x) равна -2x - 4.
- Для -1 <= x <= 1, функция f(x) равна -2.
- Для x > 1, функция f(x) равна 2x - 4.
Для каждого сегмента мы можем найти производную исходной функции по правилу дифференцирования линейной функции.
1) Для первого сегмента, где -∞ < x < -1, производная функции f(x) равна производной линейной функции -2x - 4:
f'(x) = -2.
2) Для второго сегмента, где -1 <= x <= 1, производная функции f(x) равна производной константы -2:
f'(x) = 0.
3) Для третьего сегмента, где x > 1, производная функции f(x) равна производной линейной функции 2x - 4:
f'(x) = 2.
Теперь у нас есть первые производные для всех трех сегментов функции f(x). Чтобы найти следующие производные, мы просто продолжаем дифференцировать каждый сегмент еще 8 раз.
1) Для первого сегмента:
f''(x) = 0 (производная константы равна нулю)
f'''(x) = 0 (производная нуля равна нулю)
f''''(x) = 0
f'''''(x) = 0
f''''''(x) = 0
f'''''''(x) = 0
f''''''''(x) = 0
f'''''''''(x) = 0
2) Для второго сегмента:
f''(x) = 0
f'''(x) = 0
f''''(x) = 0
f'''''(x) = 0
f''''''(x) = 0
f'''''''(x) = 0
f''''''''(x) = 0
f'''''''''(x) = 0
3) Для третьего сегмента:
f''(x) = 2 (производная линейной функции 2x - 4 равна 2)
f'''(x) = 0 (производная константы равна нулю)
f''''(x) = 0
f'''''(x) = 0
f''''''(x) = 0
f'''''''(x) = 0
f''''''''(x) = 0
f'''''''''(x) = 0
Теперь, чтобы найти 9-ю производную функции f в точке x = 0, мы должны воспользоваться знаком правила Лопиталя для определения, какой из сегментов функции f(x) будет включен в ответ.
Правило Лопиталя:
Если при вычислении производной функции для заданной точки нижняя и верхняя границы функции сходятся к одному и тому же числу, то значение производной в этой точке не меняется и равно значению производной функции в промежутке, где функции сходятся к данной точке.
Из графика видно, что при x → 0 сегменты функции f(x) сходятся к -2 и -4, что указывает на второй сегмент (-1 <= x <= 1).
Таким образом, 9-я производная функции f в точке x = 0 равна 0.