Найди рациональное выражение, областью допустимых значений (од3) которого являются все Числа.
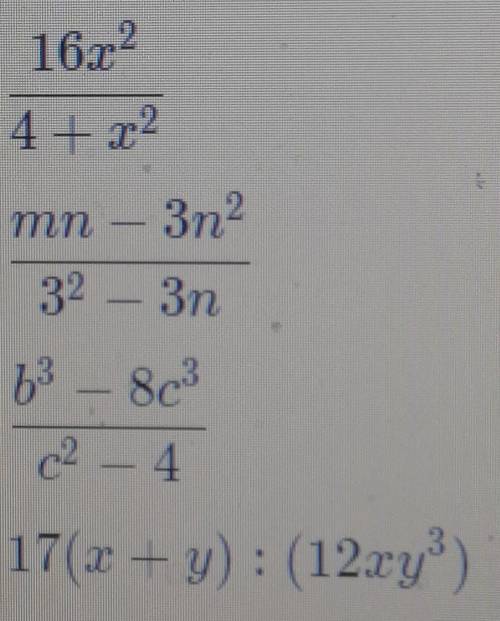
Другие вопросы по теме Математика
Популярные вопросы
- Выберите предложения, из которого невозможно вычленить ни одного словосочетания:...
2 - брусок размером 0.5 0.4 0.1 м находится в баке с глицирином на глубине...
3 - Проблема инкультурации в условиях глобальных интеграционных процессов....
3 - 19. Выбери строку, где значения величин записаны в порядке их увеличения...
1 - Сравнить музыкальные произведения Чакона И. С. Бах транскрипция Ф. Бузони...
3 - SPEAKING Work in pairs. Discuss the quiz. Do you agree or disagree with...
3 - Тақырып. Қазақстан картасы. Карта кметана. 1 Ассоциация жаа.Қазақстан2...
3 - Определите значение переменных a, b, с после ввода значений с клавиатуры...
2 - Із натуральних чисел від 1 до 24 навмання вибирабть одне.Яка ймовірність...
2 - Мне нужно сочинения про Александра Сергеевича Пушкина, на Ангисском...
3
Пошаговое объяснение:
Это 16x^2/(4+x^2) т. к. при любом х (4+x^2)>0 и дробь всегда существует
На данном изображении видно, что областью допустимых значений выражения являются все числа. То есть, ровно такое же выражение необходимо составить.
Мы можем предложить следующее рациональное выражение, областью допустимых значений которого являются все числа:
f(x) = x / (x - x + 1)
В этом выражении, переменная x может принимать любое значение, так как она находится в знаменателе и числитель равен ей.
Обоснование:
При выборе числителя, который равен переменной x, мы гарантируем, что выражение будет иметь значение для любого x.
Знаменатель выражения равен (x - x + 1), что приводит к выражению 1. Таким образом, знаменатель всегда будет равен 1, независимо от значения x.
После сокращения получаем f(x) = x / 1, что эквивалентно f(x) = x.
Таким образом, рациональное выражение f(x) = x, областью допустимых значений которого являются все числа.