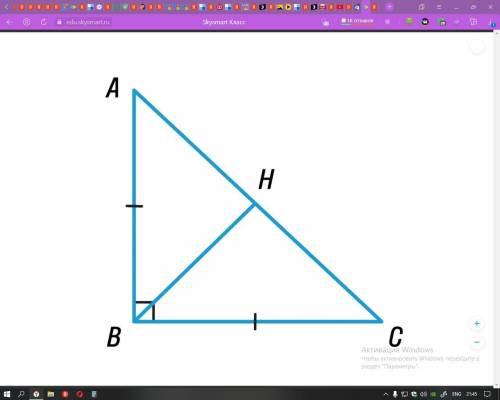
Найди bac прямоугольного треугольника abc и длину его биссектрисы если hc 8см

Для нахождения угла BAC прямоугольного треугольника ABC и длины его биссектрисы нам понадобится использовать теорему Пифагора и теорему о биссектрисе треугольника. 1. Начнем с использования теоремы Пифагора для нахождения длины гипотенузы AB: AB^2 = AC^2 + BC^2 В нашем случае из условия задачи нам дана длина высоты hc, поэтому нам известны AC и BC. По теореме Пифагора для прямоугольного треугольника AHC: AC^2 + HC^2 = AH^2 Так как HC равняется 8 см согласно условию, мы можем найти AC: AC^2 + 8^2 = AH^2 AC^2 + 64 = AH^2 (1) Аналогично, для треугольника BHC: BC^2 + HC^2 = BH^2 BC^2 + 8^2 = BH^2 BC^2 + 64 = BH^2 (2) 2. Теперь воспользуемся теоремой о биссектрисе треугольника для нахождения длины биссектрисы AI. Теорема о биссектрисе гласит, что биссектриса треугольника делит противоположную сторону пополам и равна произведению длины этой стороны на отношение длин двух других сторон треугольника. В нашем случае биссектриса AI делит сторону AC на две равные части, то есть AI = IC. Аналогично, биссектриса BI делит сторону BC на две равные части, то есть BI = IC. Длина биссектрисы AI равна произведению длины стороны AC на отношение длин сторон AB и BC: AI = AC * (AB / BC) (3) Так как нам известны длины сторон AC и AB (последнюю мы найдем в пункте 3), а также длина стороны BC, мы можем вычислить длину биссектрисы AI. 3. Для нахождения длины стороны AB воспользуемся теоремой Пифагора для прямоугольного треугольника BHA: BH^2 + AH^2 = BA^2 Из уравнения (2) мы можем найти BH^2: BC^2 + 64 = BH^2 А из уравнения (1) мы можем найти AH^2: AC^2 + 64 = AH^2 Подставим найденные значения для BH^2 и AH^2 в уравнение: BH^2 + AH^2 = BA^2 BC^2 + 64 + AC^2 + 64 = BA^2 BC^2 + AC^2 + 128 = BA^2 (4) Теперь мы можем найти длину стороны AB, просто извлекая квадратный корень: BA = √(BC^2 + AC^2 + 128) (5) 4. Вернемся к уравнению (3) для нахождения длины биссектрисы AI: AI = AC * (AB / BC) Подставим найденные значения для AC и AB: AI = AC * (BA / BC) (6) Таким образом, чтобы найти угол BAC и длину биссектрисы AI прямоугольного треугольника ABC при условии, что hc = 8 см, нам нужно выполнить следующие шаги: 1. Найдите AC, используя уравнение (1). 2. Найдите BC, используя уравнение (2). 3. Найдите BA, используя уравнение (5). 4. Найдите AI, используя уравнение (6). После выполнения этих шагов вы получите ответы на заданный вопрос.