Напишите все , которыми можно решить уравнение ниже
21+10t-t^2=0

Ответы

TanyaSha300 17.01.2022 06:00

ответ .

1) Решение через дискриминант .

$21+10t-t^2=0\ \ \ \to \ \ \ \ \ t^2-10t-21=0D=b^2-4ac=10^2+4\cdot 21=184=2\sqrt{46}t_{1,2}=\dfrac{10\pm \sqrt{184}}{2}\ \ ,\ \ t_1=5-\sqrt{46}\ ,\ \ t_2=5+\sqrt{46}$

2) Решение с выделения полного квадрата .

$21+10t-t^2=-(t^2-10t-21)=-\Big(\, (t-5)^2-25-21\Big)==-(t-5)^2+46-(t-5)^2+46=0\ \ \ \Rightarrow \ \ \ (\sqrt{46})^2-(t-5)^2=0\ \ ,(\sqrt{46}-t+5)(\sqrt{46}+t-5)=0a)\ \ \sqrt{46}-t+5=0\ \ \ \to \ \ \ t=5+\sqrt{46}\approx 11,8b)\ \ \sqrt{46}+t-5=0\ \ \ \to \ \ \ t=5-\sqrt{46}\approx -1,8$

3) Решение с теоремы Виета.

$-t^2+10t+21=0\ \ \ \Rightarrow \ \ \ \left\{\begin{array}{l}t_1+t_2=10\\t_1\cdot t_2=-21\end{array}\righ\ \ \left\{\begin{array}{l}t_2=10-t_1\\t_1\cdot (10-t_1)=-21\end{array}\righ$

$\left\{\begin{array}{l}t_2=10-t_1\\10t_1-t_1^2=-21\end{array}\righ\ \ \left\{\begin{array}{l}t_2=10-t_1\\t_1^2-10t_1-21=0\end{array}\righ$

Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .

P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения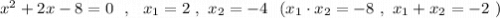 $x^2+2x-8=0\ \ ,\ \ x_1=2\ ,\ x_2=-4\ \ (x_1\cdot x_2=-8\ ,\ x_1+x_2=-2\ )$ .

4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения :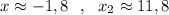 $x\approx -1,8\ \ ,\ \ x_2\approx 11,8$ .