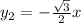Напишите уравнение асимтоты гиперболы
Другие вопросы по теме Математика
Популярные вопросы
- Какой из видов хозяйственной деятельности и почему в большой степени...
1 - Скорость течения 3,7 км/ч. какое расстояние он пройдёт, двигаясь 2 ч...
3 - Мені потрібно на завтра! твір на тему чому я пишаюсь своїм товаришем...
1 - Кратчайшее расстояние между городом баку и южным полюсом а)17286 б)18500...
2 - За 4 дня турист км. за первый день он км700м, за второй день км400м....
1 - Мы убираемся около школы. я подметаю у листья. миша, максим и кирил увозят...
1 - Коли у мадриді 17: 00, у сан-франциско 8: 00 того же дня. таня лягла...
2 - Спиши,вставив пропущенные буквы и знаки препинания.причастные обороты...
1 - Выпиши 3 пословицы великих людей, объясни их...
2 - Биссектриса угла а параллелограмма авсd пересекает сторону вс в точке...
3
Пусть уравнение асимптоты к гиперболе: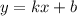 , где
, где 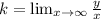 , а
, а 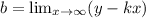
Найдём значения k и b для 2 случаев:
Случай первый:
Итого, первая асимптота: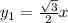
Случай второй:
Вторая асимптота: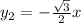
ответ: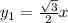 ,
,