1. Математика
  2. Напиши уравнение касательной

Напиши уравнение касательной к графику функции f(x) = х^2+ 6х +8 в точке с абсциссой х(о)= 1.

msnyamkina msnyamkina    2   20.02.2022 19:19    0

Ответы
mnize123 mnize123  20.02.2022 19:20

Уравнение касательной к графику функции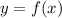 y=f(x) в точке 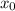x_0 имеет вид:

y_k=f(x_0)+f'(x_0)(x-x_0)

Рассмотрим функцию:

f(x) = x^2+ 6x +8

f(x_0) =f(1) =1^2+ 6\cdot1 +8=15

Находим производную:

f'(x)=2x+ 6

f'(x_0) =f'(1) =2\cdot1 +6=8

Подставляем все значения в уравнение:

y_k=15+8(x-1)

y_k=15+8x-8

\boxed{y_k=8x+7}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Webymnyaha Webymnyaha  15.04.2020 11:29
Если 21 км это 35%, то 60-это 100%?если 9,6 т это 24%, то 400-это 100%?...
sofiapel68p08lqa sofiapel68p08lqa  15.04.2020 11:29
Соберите в левой части уравнения 2х +6 = -3х - 10 все слагаемые, содержащие неизвестное, а в правой - не содержащие неизвестное 2х - 3х = -6 - 10 2х + 3х = 6 - 10 2х - 3х =...
Пацивис Пацивис  15.04.2020 11:29
3−(x+43​)=161​x (2127​−x)+83​=2...
wwwraisakravets wwwraisakravets  15.04.2020 11:29
Б) решите уравнение: 4,2у + 2,8у = 1,4...
arave1 arave1  15.04.2020 11:29
Найди решения ребуса в котором буква К равно 4. МАЛЁК + МАЛЁК РЫБКА...
ksenla200xxx ksenla200xxx  15.04.2020 11:29
Среднее арифметическое четырех чисел равно 2,25 найдите сумму этих чисел...
дншегзпгх дншегзпгх  15.04.2020 11:29
Квадрокоптор летал a ч со скоростью b км/ч. Какое расстояние он пролетел за это время...
hkarkosan3 hkarkosan3  15.04.2020 11:29
В двух бочках вместе 572л бензина. Когда из первой бочке взяли 1/3 бензина а из второй бочки взяли 3/7 бензина то в обеих бочках бензина стало поровну. Сколько литров бензина...
hekyljana156 hekyljana156  15.04.2020 11:29
РЕШИТЬ КОНТРОШУ 1.Решить неполное квадратное уравнение: а) 2х² - 128 = 0; б) 8х² - 3х = 0. 2.Решить уравнение: а) х² - х – 20 = 0; б) 3х² - 2х – 8 = 0; в) х² + 6х – 2 = 0; г)...
Фахрияlove1 Фахрияlove1  15.04.2020 11:29
Яке число більше за 5.74 менше від 5.76...

Популярные вопросы