написать уравнение касательной к графику функции f(x)= -1 в точке с абсциссой x0=-1
-1 в точке с абсциссой x0=-1
Другие вопросы по теме Математика
Популярные вопросы
- Составьте уравнения (в молекулярном и ионном виде) возможных химических реакций...
1 - Высота наклонной плоскости 1,2 м, а длина 12 м. Для подъема по ней груза весом...
2 - Ардагерлерімізді ардақтайық мақала...
3 - Укажите верную пару «регион современного оттока населения-регион современного...
2 - 1. Выполни деление.70 км 256 м:818 кг 712 г: 29т 704 кг : 4...
2 - ) составьте диалог , в котором обсудите проблему Глобального изменения климата:К...
2 - с англ Задание1. Напишите глаголы в скобках в Past Simple (в времени), добавив...
2 - Роберт Шуман – немецкий композитор, родился в 1810, умер в 1856. Несмотря на сильное...
3 - КМ и KN - отрезки касательных, проведенных из точки К к окружности с центром О....
2 - Что видит Ассоль в каждом человеке?...
1
y = 3x+1
Пошаговое объяснение:
Уравнение касательной к функции выглядит так: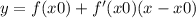
найдём производнуюf(x):
Далее подставим x0 в уравнение касательной: