Намалювати графік та обчислити площу фігури яка вийшла. Нарисовать график, и отчислить площадь фигуры которая вышла.

Другие вопросы по теме Математика
Популярные вопросы
- За покупку 2 кг риса по 3 1/4 рубля за килограмм коля заплатил 10 рублей....
1 - 1.чашка и блюдца стоят 25 руб,а4 чашки и 3 блюдца стоят 88 руб.сколько...
3 - 10 машин выпускают одинаковые резиновые мячи по 10 г каждый.одна из машин...
3 - Ширина прямоугольника8см,что составляет 4/5длины.найти площадь и периметр...
3 - Система отношений, связанных с обменом товаров и услуг; место купли-продажи....
1 - Знайти відношення значень величин 3км до 4км...
1 - Утрьох цистернах було 10720 л пального. у першій і третій разом було 7870л,...
1 - Решить с уравнения 5 ласс. с мешка взяли 25 кг. сахара а потом еще два...
3 - Основные темы романа л.н.толстого война и мир...
2 - Во дворе куры,петухи и утки.всего-21 птица.петухов в 10 раз меньше,чем...
2
Пошаговое объяснение:
там, где будем менять пределы интегрирования, обозначать буду
нижний предел верхний предел
верхний предел 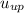
1)
2) здесь площадь считаем как сумму площадей "верхней" части + "нижней" части (они равны)
3)
* порядок файлов соответствует номеру задания