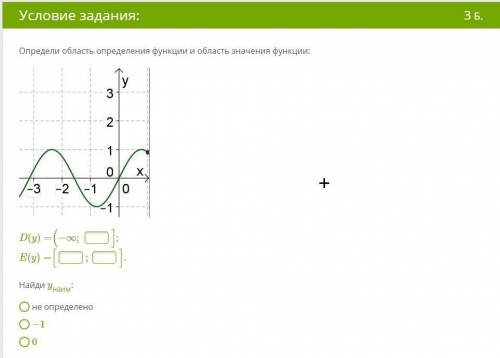
надо сделать Определи область определения функции и область значения функции:

Чтобы определить область определения (ОО) функции, нам нужно определить все значения аргумента x, при которых функция определена (не будет деления на ноль и не будет других ограничений).

В данной функции у нас есть знаменатель дроби, поэтому чтобы избежать деления на ноль, выражение в знаменателе должно быть неравным нулю:

2x - 4 ≠ 0

Теперь найдем, при каких x это уравнение не выполняется:

2x ≠ 4

x ≠ 2

Таким образом, область определения функции (ОО) - это все значения x, кроме 2.

Теперь перейдем к определению области значений (ОЗ) функции. Чтобы найти область значений, мы должны найти все возможные значения y, которые могут быть получены как результат подстановки различных значений x в функцию. В данной функции у нас имеется дробь, и она будет принимать все значения, кроме нуля.

Давайте посмотрим, что происходит с функцией, если x стремится к бесконечности (x → ± ∞):

lim (x → ± ∞) (2x-4)/(x-2)

Если мы поделим все слагаемые на x, получим:

lim (x → ± ∞) (2 - 4/x)/(1 - 2/x)

После вынесения наибольшего степенного члена - 2, получим:

lim (x → ± ∞) 2(1 - 2/x)

Теперь, когда x стремится к бесконечности, можно сказать, что дробь 2/x стремится к нулю, поэтому у нас остается только:

lim (x → ± ∞) 2(1) = 2

Таким образом, функция принимает все значения, кроме 2.

Итак, область определения (ОО) функции - все значения x, кроме 2, а область значений (ОЗ) функции - все значения y, кроме 2.