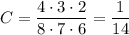На восьми карточках написаны цифры от 1 до 8 . Наугад вынимают 3 карточки. Найти вероятности событий: A= {вынута карточка с цифрой 1 },

B= {только на одной карточке чётная цифра},

C= {на всех вынутых карточках цифры менее пяти}.

Пошаговое объяснение:

Всего вариантов последовательно выбрать три карточки: 8 * 7 * 6 (вытянули одну из восьми — осталось семь — затем осталось шесть).

A) Карточка с цифрой 1 может быть вытянута первой, второй или третьей. Тогда в каждом случае осталось семь карточек, а затем шесть: 1 * 7 * 6 + 7 * 1 * 6 + 7 * 6 * 1 = 3 * 7 * 6. Вероятность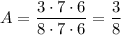

B) Чётная карточка может быть вытянута первой, второй или третьей, чётных цифр всего 4 (2, 4, 6, 8). Значит, существует четыре варианта вытянуть чётную карточку, затем остаётся четыре нечётных, затем — три нечётных. То есть подходящих вариантов 4 * 4 * 3 + 4 * 4 * 3 + 4 * 3 * 4 = 4 * 4 * 3 * 3. Вероятность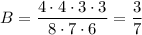  

С) Сначала вытянули одну из четырёх нужных карточек, затем — одну из оставшихся трёх, затем — одну из оставшихся двух. Нужных вариантов: 4 * 3 * 2. Вероятность