1. Математика
  2. На сколько процентов увеличится

На сколько процентов увеличится площадь квадрата если его периметр увеличить на 32%

Ксюша8800 Ксюша8800    2   02.08.2022 01:55    9

Ответы
bomberdire bomberdire  02.08.2022 01:56

Площадь квадрата увеличится на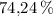 74{,}24\,\%

Пошаговое объяснение:

Если периметр квадрата был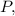 P, а стал 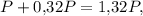P + 0{,}32P = 1{,}32P, то сторона квадрата была 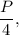\displaystyle\frac{P}{4}, а стала

\displaystyle\frac{{1{,}32P}}{4} = \displaystyle\frac{{33P}}{{100}}.

Тогда площадь квадрата была

{\left( {\displaystyle\frac{P}{4}} \right)^2} = \displaystyle\frac{{{P^2}}}{{16}},

а стала

{\left( {\displaystyle\frac{{33P}}{{100}}} \right)^2} = \displaystyle\frac{{1089{P^2}}}{{10000}}.

Значит она увеличилась на

\displaystyle\frac{{1089{P^2}}}{{10000}} - \displaystyle\frac{{{P^2}}}{{16}} = \displaystyle\frac{{1089{P^2}}}{{16 \cdot 625}} - \displaystyle\frac{{{P^2}}}{{16}} = \displaystyle\frac{{1089{P^2} - 625{P^2}}}{{16 \cdot 625}} =\\ \\=\displaystyle\frac{{464{P^2}}}{{16 \cdot 625}} = \displaystyle\frac{{16 \cdot 29{P^2}}}{{16 \cdot 625}} = \displaystyle\frac{{29{P^2}}}{{625}},

что составляет

\left( {\displaystyle\frac{{29{P^2}}}{{625}}} \right):\left( {\displaystyle\frac{{{P^2}}}{{16}}} \right) \cdot 100\,\% = \displaystyle\frac{{464}}{{625}} \cdot 100\,\% = \displaystyle\frac{{1856}}{{25}}\,\% = 74{,}24\,\% .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
алгебра171 алгебра171  12.05.2020 12:51
Выбери соответствующее данному утверждению выражение:Произведение числа 7 и суммы чисел c и d1)c*d+72)7*(c+d)3)7*(c:d)4)7*c:d5)(7+c)*d​...
alinahan444 alinahan444  12.05.2020 12:51
Начертите острый угол COD. Отметьте на луче ОD точку P и проведите через неё прямые, перпендикулярные прямым OD и OC....
YanaTsaruk YanaTsaruk  12.05.2020 12:51
Сколько делителей у числа 3 в 6 степени умножить на 5 в 4 степени с пояснениями!!...
DashaKhodenkova DashaKhodenkova  12.05.2020 12:51
Установіть відповідність між кутом при вершині осьового перерізу...
ruslapanazavr ruslapanazavr  12.05.2020 12:51
(x+320)-245=453 i 912-( p+39)=625 знайти корінь. До ть з домашніми завданнями...
viktoria050504 viktoria050504  12.05.2020 12:50
А) Запишите в виде десятичной дроби: 9%, 40%, 250%.6) Запишите в виде процентов: 0,04; 1,2; 0,5.​...
katerinasem251 katerinasem251  12.05.2020 12:50
Какую часть составляет от 1 дм а) 1 см, б) 5 см, в) 3см, г) 7см...
thankay thankay  12.05.2020 12:50
сдать должен к 13:00 по Москве)...
dimaandreevich dimaandreevich  12.05.2020 12:50
Решите задачу В зоопарке есть красные, жёлтые и зелёные попугаи (есть хотя бы по одному попугаю каждого из перечисленных цветов; попугаев других цветов в зоопарке нет). Известно,...
верника3 верника3  23.06.2021 14:03
Нужно решить методом бернулли...

Популярные вопросы