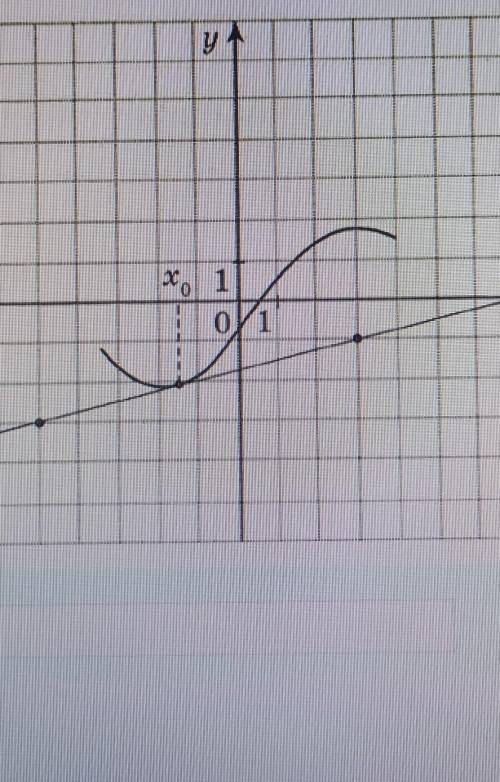
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой хо. Найдите значение производной функции f(x) в точке хо.​

1) касательная к графику имеет "положительный" наклон - т.е искомая производная должна быть со знаком +

2) отношение приращения значения функции к приращению аргумента (из графика): 1/4,5 или 2/9. А это и есть значение производной.

УДАЧИ!

Пошаговое объяснение:

Пошаговое объяснение:

напишем уравнение касательной

это прямая, проходящая через две точки (они отмечены на графике)

точка (-5; -3) и точка (3; -1)

теперь приведем это уравнение в тот вид, который нам надо

а надо нам уравнение с угловым коэффициентом y = kx+b, потому как этот угловой коэффициент и есть значение производной в точке х₀, т.е f'(x₀)=k

таким образом f'(x₀)= 0,25