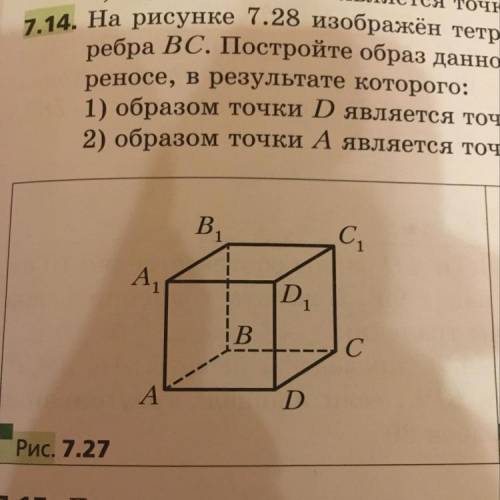
На рисунке 7.27 изображен куб ABCDA1B1C1D1. Постройте образ данного куба при параллельном переносе, в результате которого: 1) образом точка А является точка D
2) образом точки B является точка C1

Чтобы построить образ данного куба при параллельном переносе, воспользуемся следующими шагами:

1) Образом точка A является точка D:
- Найдем вектор переноса, который определяется разностью координат точек D и A.
В данном случае, DA = (2, 3, 0) - (0, 0, 0) = (2, 3, 0).
- При параллельном переносе все точки куба смещаются на одинаковое расстояние вдоль данного вектора.
То есть, для каждой точки куба, необходимо добавить вектор переноса DA.
Например, координаты точки B1 с учетом переноса будут BC1 = (1, 1, 3) + (2, 3, 0) = (3, 4, 3).
По аналогии, найдем новые координаты остальных точек куба:
- А1D1 = A1D + DA = (0, 2, 1) + (2, 3, 0) = (2, 5, 1)
- C1B1 = C1B + DA = (0, 0, 2) + (2, 3, 0) = (2, 3, 2)
- C1D1 = C1D + DA = (1, 0, 3) + (2, 3, 0) = (3, 3, 3)
- B1A1 = B1A + DA = (1, 1, 3) + (2, 3, 0) = (3, 4, 3)
- D1C1 = D1C + DA = (3, 0, 1) + (2, 3, 0) = (5, 3, 1)

Таким образом, образом точка А будет точка D, а новые координаты остальных точек куба:
A1(2, 5, 1), B1(3, 4, 3), C1(2, 3, 2), D1(5, 3, 1).

2) Образом точки B является точка C1:
- Аналогично предыдущему пункту, найдем вектор переноса BC1, который определяется разностью координат точек C1 и B.
В данном случае, BC1 = (2, 3, 2) - (1, 1, 3) = (1, 2, -1).
- Добавим вектор переноса BC1 к каждой точке куба:
- AB1 = AB + BC1 = (0, 0, 3) + (1, 2, -1) = (1, 2, 2)
- AC1 = AC + BC1 = (1, 0, 0) + (1, 2, -1) = (2, 2, -1)
- AD = AD + BC1 = (2, 3, 0) + (1, 2, -1) = (3, 5, -1)
- A1B1 = A1B + BC1 = (1, 1, 3) + (1, 2, -1) = (2, 3, 2)
- A1C1 = A1C + BC1 = (2, 3, 2) + (1, 2, -1) = (3, 5, 1)
- A1D1 = A1D + BC1 = (0, 2, 1) + (1, 2, -1) = (1, 4, 0)

Таким образом, образом точка B будет точка C1, а новые координаты остальных точек куба:
A1(2, 5, 1), B1(2, 3, 2), C1(3, 5, 1), D1(1, 4, 0).

Надеюсь, данное разъяснение помогло вам понять, как производится параллельный перенос и как находить образы точек при таком переносе. Если у вас остались вопросы, не стесняйтесь задать их!