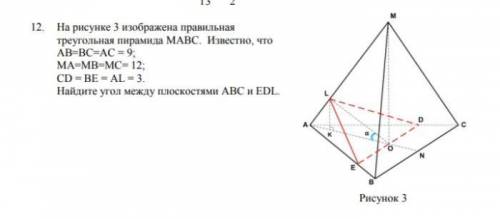
На рисунке 3 изображена правильная треугольная пирамида MABC. Известно, что AВ=BC=AC = 9; MA=MB=MC= 12; CD = BE = AL = 3. Найдите угол между плоскостями ABC и EDL.
Другие вопросы по теме Математика
Популярные вопросы
- Склади формулу, яка виражає залежність змінної у відзмінної х.х 1 2...
3 - Защитными при бактерии являются...
3 - осталось меньше часа Прочитай предложение и вставь нужный артикль «a»,...
3 - Кузьма Иванович положил 15 тыс. руб. на вклад «Выгодный». Через год...
3 - В треугольнике АВС внешний угол при вершине В на 46 больше внешнего...
2 - К основным свойствам ощущений не относится : а) качество, б) интенсивность,...
3 - Разберите возвратнве местоимения себе, себя как часть речи....
2 - Ж) 5/12− 7/9 у=10. 5/12−3 у...
2 - Найдите сравнения (сравнительный оборот) и выпишите. 1. От его тяжести...
1 - Дано m(солі0= 5г m(розчину)=250г Знайти W(солі)=? W (солі) = 5г / 250г...
2
Заметим, что треугольники ABC, MAB и MBC являются равносторонними, так как их стороны имеют одинаковую длину. Также, треугольник AMD, BMD и CMD в плоскости ABC также являются равносторонними, так как их стороны равны.
Решим задачу шаг за шагом:
Шаг 1: Найдем длину AD.
Так как треугольник AMD равносторонний, то мы можем использовать теорему Пифагора для нахождения длины AD. Найдем длину MD по теореме Пифагора в прямоугольном треугольнике MCD:
MD² = MC² - CD²
MD² = 12² - 3²
MD² = 144 - 9
MD² = 135
MD = √135
MD = 3√15
Так как MA = MD + AD, то
AD = MA - MD
AD = 12 - 3√15
Шаг 2: Найдем угол BCD.
В треугольнике BCD, мы можем использовать теорему косинусов, чтобы найти угол BCD. Так как BС = СD = 9, а BD = 2CD, то
BD = 2*9 = 18
Используя теорему косинусов, получаем:
cos(BCD) = (BC² + CD² - BD²) / (2 * BC * CD)
cos(BCD) = (9² + 9² - 18²) / (2 * 9 * 9)
cos(BCD) = (81 + 81 - 324) / 162
cos(BCD) = (162 - 324) / 162
cos(BCD) = -162 / 162
cos(BCD) = -1
Так как угол BCD находится в первой четверти, то угол BCD равен 180° - arccos(-1) = 180° - 180° = 0°.
Шаг 3: Найдем угол EDL.
Угол EDL равен углу BCD, так как сторона DL параллельна стороне BC и L также лежит на плоскости ABC.
Таким образом, угол между плоскостями ABC и EDL равен 0°.