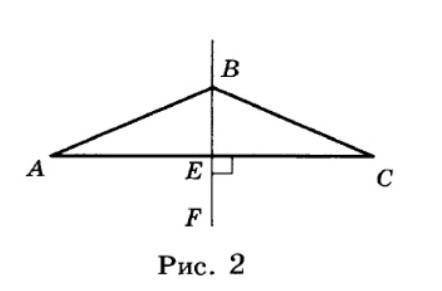
На рисунке 2 AB=BC , <FEC=90° , AE=10дм., <ABC=130°30'. Найдите AC и <EKB с решением задачи и отсылкой на свойства)​

Добрый день! Для решения данной задачи нам потребуются свойства треугольника и правильность построения.

1. Из условия задачи известно, что AB = BC. Значит, треугольник ABC является равнобедренным, и угол BAC равен углу BCA.

2. Также из условия задачи известно, что угол FEC равен 90 градусам. Это означает, что треугольник FEC является прямоугольным.

3. Теперь рассмотрим треугольник ACE. Мы знаем, что его сторона AE равна 10 дм. Также из свойства прямоугольного треугольника следует, что угол EAF является прямым. Значит, по теореме Пифагора мы можем найти сторону AC.

AC² = AE² + EC²
AC² = 10² + EC²
AC² = 100 + EC²

4. Итак, у нас остается найти сторону EC. Для этого рассмотрим треугольник ABC. Мы знаем, что угол ABC равен 130 градусам 30 минутам. Вершина E находится на продолжении стороны AB за точкой B. Значит, угол BEA равен 180 градусам минус угол ABC.

Угол BEA = 180° - 130° 30' = 49° 30'

Также у нас есть равенство углов ABE и EBA, так как треугольник ABC равнобедренный.

5. В треугольнике ABE мы знаем две стороны - AE = 10 дм и угол ABE = 49 градусов 30 минут. Для нахождения стороны EC мы можем использовать закон синусов:

EC / sin(49°30') = AE / sin(180° - (49°30'))
EC / sin(49°30') = AE / sin(130°30')
EC = AE * sin(49°30') / sin(130°30')

6. Теперь, зная значение стороны EC, можно подставить его в уравнение для AC^2 и получить значение AC:

AC² = 100 + EC²
AC² = 100 + (AE * sin(49°30') / sin(130°30'))²
AC = √(100 + (10 * sin(49°30') / sin(130°30'))²)

7. Также в условии задачи нам нужно найти угол EKB. Мы знаем, что треугольник BEC является прямоугольным (угол FEC = 90°) и из треугольника ABC следует, что угол EBC равен углу BAC. Мы уже знаем значение угла BAC, так как треугольник ABC равнобедренный. Значит, мы можем найти угол EKB как разность между углом EBC и углом FEC:

Угол EKB = (угол EBC) - (угол FEC)
= (угол BAC) - 90°

Теперь, если нам известны значения угла BAC и сторон AB и BC, мы можем точно посчитать значение угла EKB.

В результате решения задачи мы сможем найти значения стороны AC и угла EKB с помощью приведенных выше шагов и применения соответствующих свойств треугольников.