На рисунке 14.25 показан метод определения ширины реки AD путем локального построения двух похожих треугольников ABC и DEC. Если BC составляет 50 м, EC = 16 м, DC = 17 м, найдите расстояние AD.
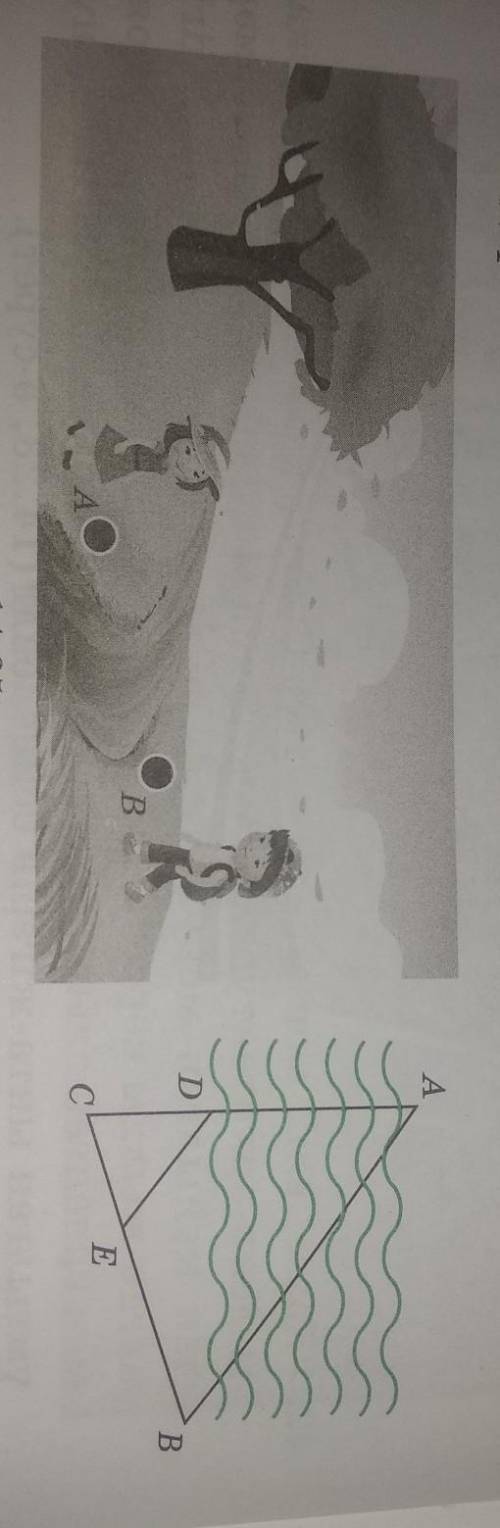
Ответы
Для решения этой задачи, мы можем использовать свойство похожих треугольников с равными пропорциями и соотношениями сторон.
В данном случае, мы имеем треугольники ABC и DEC. Мы знаем, что они являются похожими треугольниками, так как у них имеются два угла с одинаковой мерой: угол ABC и угол DEC.
Мы можем использовать соотношение сторон похожих треугольников, чтобы найти расстояние AD.
Соотношение сторон похожих треугольников можно записать как:
AC/DE = BC/DC
где AC и DE - соответствующие стороны треугольников ABC и DEC, а BC и DC - известные стороны треугольника.
Известными значениями в данной задаче являются:
BC = 50 м,
EC = 16 м,
DC = 17 м.
Нам нужно найти расстояние AD.
Определим соотношение сторон:
AC/DE = BC/DC
Подставим известные значения:
AC/16 = 50/17
Перекроим пропорцию, чтобы избавиться от дроби:
AC * 17 = 16 * 50
AC * 17 = 800
Теперь найдем значение AC, разделив обе стороны уравнения на 17:
AC = 800 / 17
AC ≈ 47,06 м
Таким образом, ширина реки AD составляет около 47,06 метров.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Популярные вопросы
- Определите силу тока в медном проводнике , через который поперечное...
2 - Переведите на язык, только не через переводчик в россии есть верующие...
1 - Янемогу решить .дети собрали 93яблока ,87груш и 129слив. каждый...
2 - Условие .у коли было 5р и3р.он куптл ручки за 3р.сколько денег осталось...
2 - Перевести текст айтжан дастарқан басында анасына: сен осы шайды...
3 - Можно ли считать за материальную точку: 1) ракету на орбите 2)летящую...
1 - Запиши число которое в натуральном ряду следует за числом: 1) 72;...
3 - 2-(1 11/30-1,7)×1 2/7÷1 13/14= ,решите , распишите по действиям,заранее...
3 - Текст на пословицу умные речи приятно слушать...
1 - Что характеризирует температура? ( 8 класс)...
2