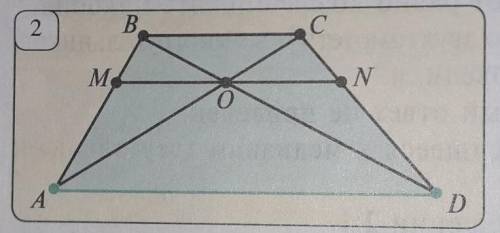
На рис. 2 AD||ВС||MN. Найдите отрезок MN, если ВС = 6 см, AD = 10 см
Другие вопросы по теме Математика
Популярные вопросы
- Магнит вводят в кольцо, в результате чего появляется ток, направление которого...
2 - При равновесии рычага на его меньшее плечо действует сила 3кН, на большее 4,5...
1 - Рассчитай толщину прозрачной пластины, если время, за которое нормально падающий...
3 - В начальный момент в первой куче было 5 камней, во второй куче – S камней; 1...
1 - Составь подмножество множества А по самостоятельно установленному признаку....
2 - «Моральна справедливість – чи існує вона?»(7-9 речень)...
1 - Questions: 1. What is the largest country in the world? 2. What is the name...
1 - Напишите уравнения следующих ядерных реакций: алюминий (27 13Al) бомбардируется...
3 - Прочитай тексты. О ком в них рассказыватся? Определи тему. 2 класс русский язык...
3 - Разложите на множители 0,25t^2-(t+p)^2...
3
Задача 1.
Большее основание трапеции равно 8 см, а меньшее на 3 см меньше средней линии.
Найти: ВС, МК.
Дано:
ABCD - тоапеиия. AD = 8 см. МК - соедняя линия. ВС - ? на 3 см меньше МК.
Найти: ВС, МК.
Решение:
Пусть ВС = x см, тогда МК = (х + 3) см
МК = (AD + ВС) : 2; х + 3 = (х + 8) : 2; 2х + 6 = х + 8; х = 2.
ВС = 2 см,
МК = 2 + 3 = 5 (см)
ответ: ВС = 2 см, МК = 5 см.
Задача 2.
В равнобокой трапеции диагональ делит острый угол пополам. Периметр трапеции равен 54 дм, большее ее основание - 1,8 м. Вычислите меньшее основание трапеции.
Дано: ABCD - равнобокая трапеция. Р = 54 дм. AD = 1,8 м = 18 дм.
Найти: ВС.
Решение:
∠1 = ∠2 так как АС - биссектриса ∠А; ∠2 = ∠3, как внутренние накрест лежащие углы.
∠1 = ∠2 и ∠2 = ∠3 => ∠1 = ∠3 => ∆АВС - равнобедренный.
Пусть АВ = ВС = CD = х.
Уравнение:
3х + 18 = 54
3х = 54 - 18
3х = 36
х = 12
ответ: ВС = 12 дм.
Задача 3.
В равнобокой трапеции с острым углом 60° биссектриса этого угла делит меньшее основание, равное 16 см, пополам. Найдите среднюю линию трапеции.
Дано:
ABCD - равнобокая трапеция, ВС = 16 см.
АК - биссектриса ∠А
ВК = КС
МN - средняя линия
∠А = 60°
Найти: MN.
Решение:
Так как К - середина ВС, то ВК = КС = ВС : 2 = 16 см : 2 = 8 см.
Так как АК - биссектриса КА, то ∠1 = ∠2; ∠2 = ∠3 как внутренние накрест лежащие углы.
∠А = ∠D, АВ = CD, ∆AВЕ = ∆DCF (по гипотенузе и острому углу).
Значит, АЕ = DF, ∠АВЕ = 30°, ∆AВЕ - прямоугольный.
АЕ = АВ : 2; АЕ = 8 : 2 = 4 см.
DF = 4 см, EF = ВС = 16 см, AD = 16 + 4 + 4 = 24 см.
MN = (ВС + AD) : 2 = (16 + 24) : 2 = 20 см.
ответ: MN = 20 см