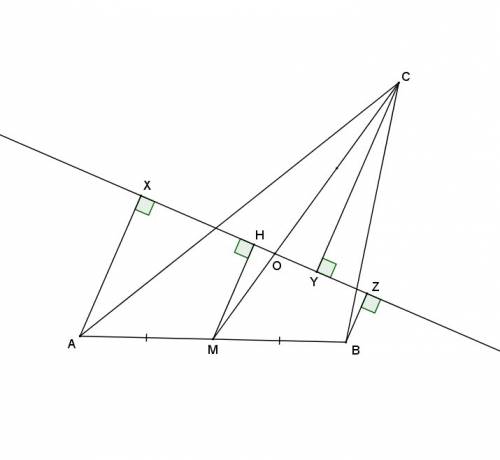
На прямую, проходящую через точку пересечения медиан треугольника медиан треугольника abc и пересекающую сторону ca и cb, опущены перпендикуляры ax, bz и cy. докажите что cy = ax+bz

Из середины М стороны АВ опустим еще перпендикуляр МН на эту прямую. Тогда АВZX - прямоугольная трапеция и MH=(AX+BZ)/2 - ее средняя линия. Если О - точка пересечения медиан, то треугольники МОH и  COY подобны по двум углам, а значит CY/MH=CO/MO=2 по свойству медиан. Итак, CY=2MH=AX+BZ. Если вдруг окажется, что H=O=Y, т.е. МОH и  COY не треугольники, то все равно CY=2MO=2MH.