на простой интеграл , с подробным объяснением
Другие вопросы по теме Математика
Популярные вопросы
- решить контрольную по химии 9 класс...
3 - Наибольший общий делитель. Взаимно простые числа. Наименьший общий...
3 - Кроссворд на тему - иглокожие по словами ( только вопросы ) Иглокожие,...
1 - Сколько будет 8858566+6888+68866х67899-245667-79...
1 - . В какую сторону сместится равновесие в системе С2Н4(г) + Н2О (г)...
1 - 1. К пуриновым азотистым основаниям , входящим в состав РНК , относятся:...
1 - ть будьласка хто відповість ві ів...
2 - Тема: Пирамида. Свойства пирамиды...
2 - Use the gerund of the verb in brackets: a) in the active or passive...
2 - Основание пирамиды SABC— равнобедренный прямоугольный треугольник ABC(...
3
Имеем подынтегральное выражение: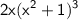
[Формула куб суммы: ]
]
Раскроем скобки, и распишем как куб суммы.
как куб суммы.
Значит,
Теперь нам будет проще интегрировать. Нам потребуется следующее правило интегрирования:
Интегрируем: