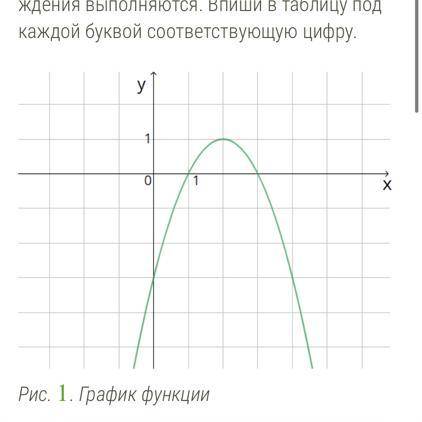
На координатной плоскости изображён график функции вида y=ax^2+bx+c
Установи соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впиши в таблицу под каждой буквой соответствующую цифру.
УТВЕРЖДЕНИЯ:
А) функция возрастает на промежутке; Б) функция убывает на промежутке.
промежутки:
1 )[−1;3]
2)[−1;1]
3)[2;4]
4)[1;3]
Запиши в ответе цифры расположив их в порядке, соответствующем буквам:
А , Б
Другие вопросы по теме Математика
Популярные вопросы
- Решить два примера углом 10.735 : 113 и 10.735 : 5...
1 - Основанием прямой призмы abcda1b1c1 является равнобедренный треугольник...
2 - Подскажите ответ примера: 4 целых 7-мь 15-ых минус 2 целые 11-ть...
3 - Найти объем параллелепипеда, основой которого есть прямоугольник...
3 - Масса пустого бидона равна 27 килограмм. если наполнить молоком...
2 - Какая из представленных электронных конфигураций соответствует 11na?...
2 - Составить слово из данных букв: e/i/f/g/r/z/n/e...
3 - Стело массой 50 кг соскользнув с наклонной плоскости, проехало по...
1 - Сумма трех чисел 24 1/2,одно число больше второго в 3 1/2 раз,третье...
3 - Определите спряжение выделенных глаголов. докажите почему так. заглянули...
1
На основании графика функции можно сделать следующие выводы:
1) Между точками x=-1 и x=1 функция возрастает. Для этого сравниваем значения функции f(x) в точках x=-1 и x=1. На графике видно, что значение функции при x=-1 меньше, а при x=1 больше, следовательно, функция возрастает на этом промежутке.
2) Между точками x=1 и x=3 функция убывает. Сравниваем значения функции при x=1 и x=3. На графике видно, что значение функции при x=1 больше, а при x=3 меньше, следовательно, функция убывает на этом промежутке.
3) Между точками x=3 и x=4 функция снова возрастает. Сравниваем значения функции при x=3 и x=4. На графике видно, что значение функции при x=3 меньше, а при x=4 больше, следовательно, функция возрастает на этом промежутке.
Таким образом, соответствие между утверждениями и промежутками будет следующим:
А) функция возрастает на промежутке [−1;1], [3;4]
Б) функция убывает на промежутке [1;3]
Ответ: 1Б, 2А, 3Б, 4А