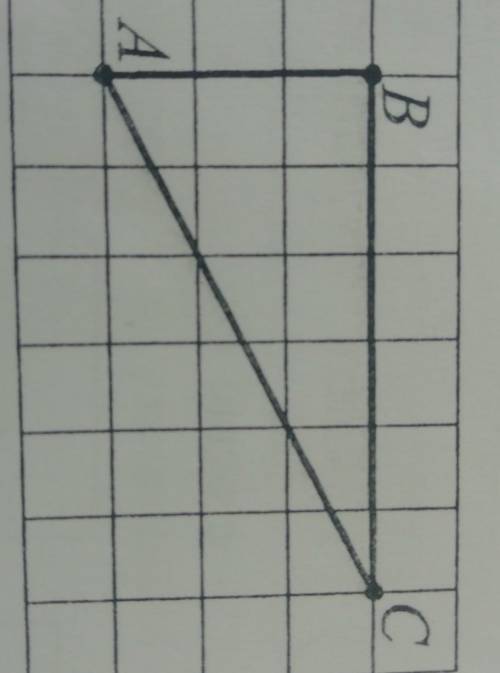
на клетчатой бумаге с размером клетки 1х1 нарисован треугольник ABC. AM - МЕДИАНА ДАННОГО ТРЕУГОЛЬНИКА НАЙДИТЕ ДЛИНУ ОТРЕЗКА BM​

Для решения этой задачи, нам нужно понять, что означает медиана треугольника и использовать его свойства.

Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В данной задаче, нам нужно найти длину отрезка BM, который является медианой треугольника ABC.

Допустим, точка M - середина стороны AC. Мы хотим найти длину отрезка BM.

По свойству медианы треугольника, медиана делит сторону треугольника, к которой она проведена, на две равные части. То есть, AM = MC.

Поскольку М - середина стороны AC, длина стороны AC равна сумме длин отрезков AM и MC. Обозначим эту длину как 2d, где d - длина отрезка AM (или MC).

Теперь обратимся к треугольнику ABC. Из условия задачи мы знаем, что сторона AB равна 10. Поскольку AM = MC, то длина отрезка AM также равна d.

Теперь, чтобы найти длину отрезка BM, нам нужно найти длину отрезка AC. Мы знаем, что длина стороны AC равна 2d. Кроме того, мы видим, что AM и BM являются биссектрисами треугольника ABC. Это означает, что точка B делит сторону AC на две части в пропорции длин AM и MC.

Поскольку AM = MC = d, точка B делит сторону AC на две части, каждая из которых равна d. Следовательно, длина отрезка AC будет равна 2d.

Таким образом, мы нашли, что длина стороны AC равна 2d, где d - длина отрезков BM и AM. В задаче нам нужно найти длину отрезка BM, поэтому мы должны найти значение переменной d.

Для этого, мы можем использовать теорему Пифагора для прямоугольного треугольника ABC. Мы видим, что стороны AB и AC являются катетами этого треугольника, а сторона BC является гипотенузой.

По теореме Пифагора, сумма квадратов длин катетов равна квадрату длины гипотенузы. Таким образом, мы можем записать следующее:

AB^2 + AC^2 = BC^2

Изначально мы знаем, что AB = 10 и длина стороны AC равна 2d. Мы хотим найти значение переменной d, поэтому мы заменяем AB и AC на известные значения:

10^2 + (2d)^2 = BC^2

100 + 4d^2 = BC^2

Теперь, чтобы найти значение длины стороны BC (то есть гипотенузы треугольника ABC), нам нужно знать длину отрезка BM.

Согласно свойству медианы треугольника, медиана также делит гипотенузу на две равные части. Это значит, что длина отрезка BC равна удвоенной длине отрезка BM. То есть:

BC = 2 * BM

Теперь мы можем заменить значение BC в уравнении:

100 + 4d^2 = (2 * BM)^2

100 + 4d^2 = 4 * BM^2

25 + d^2 = BM^2

Теперь, чтобы найти длину отрезка BM, нам нужно решить это уравнение и найти значение переменной BM.

Но у нас не хватает информации о треугольнике ABC. Мы не знаем длину стороны BC или угол между сторонами AB и AC. Без этой информации, мы не можем найти конкретное значение длины отрезка BM или выразить его в виде числа.

Однако, мы можем записать решение уравнение в общем виде, используя переменную x для значения длины отрезка BM.

25 + d^2 = x^2

Таким образом, мы получаем квадратное уравнение, которое можно решить, если у нас будет дополнительная информация о треугольнике ABC.

В заключение, чтобы найти длину отрезка BM (медианы треугольника), нам необходима дополнительная информация о треугольнике ABC. В данном случае, без знания длины стороны BC или угла между сторонами AB и AC, мы не можем найти конкретное значение длины отрезка BM.