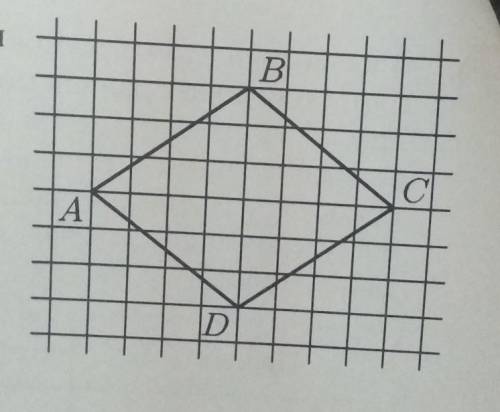
На клетчатой бумаге с размером клетки 1х1 изображён
ромб ABCD. Найдите его периметр.​

Чтобы найти периметр ромба ABCD на клетчатой бумаге, нам нужно знать длину сторон этого ромба.

В данном случае, чтобы найти длину стороны ромба, мы можем воспользоваться теоремой Пифагора.

Периметр ромба является суммой всех его сторон. Так как ромб ABCD является четырехугольником, его периметр равен сумме длин всех четырех сторон.

Для нахождения длины стороны ромба мы можем использовать длину диагонали ромба. Диагонали ромба пересекаются под прямым углом и делят его на четыре равных треугольника.

Из заданного изображения мы видим, что диагонали ромба ABCD равны 3 клеткам и 4 клеткам соответственно. При этом каждая клетка соответствует одной стороне ромба.

Теперь мы можем рассчитать длину стороны ромба, используя найденные длины диагоналей:

1) Диагонали ромба ABCD равны 3 клеткам и 4 клеткам соответственно. При этом каждая клетка соответствует одной стороне ромба.

2) Так как каждая диагональ является гипотенузой прямоугольного треугольника (с катетами, равными половинам длины диагоналей), мы можем использовать теорему Пифагора для нахождения длины стороны ромба.

Для первой диагонали, где гипотенуза равна 3 клеткам, мы можем рассчитать длину стороны ромба следующим образом:

a^2 = (3/2)^2 + (3/2)^2,
a^2 = 9/4 + 9/4,
a^2 = 18/4,
a^2 = 9/2,
a = √(9/2) = √9/√2 = 3/√2 = (3√2)/2.

Для второй диагонали, где гипотенуза равна 4 клеткам, мы можем рассчитать длину стороны ромба следующим образом:

a^2 = (4/2)^2 + (4/2)^2,
a^2 = 16/4 + 16/4,
a^2 = 32/4,
a^2 = 8/2,
a = √(8/2) = √8/√2 = 2√2/2 = √2.

Мы получили, что длина стороны ромба ABCD равна (3√2)/2 и √2 соответственно.

3) Теперь, чтобы найти периметр ромба, мы должны сложить длины всех его сторон:

Периметр = (3√2)/2 + √2 + (3√2)/2 + √2
= 3√2 + 2√2 + 3√2 + 2√2
= 8√2.

Таким образом, периметр ромба ABCD на клетчатой бумаге равен 8√2.