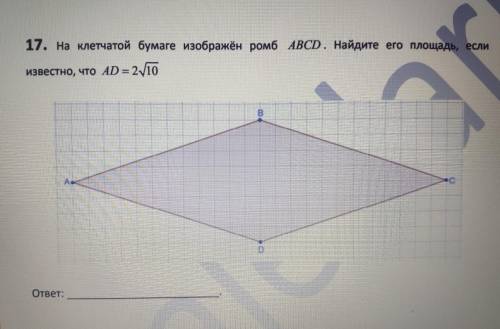
На клетчатой бумаге изображён ромб ABCD. Найдите его площадь, если известно, что AD= 2√10.
Другие вопросы по теме Математика
Популярные вопросы
- Номер 6.7 четные сократить дробь ...
2 - Примеры идиоадаптации у серой вороны. 10 и более....
3 - Составить общий вопрос the next morning i woke up on the beach...
3 - Поставь ударение ,где это нужно.обозначь орфаграмму , безударные гласные...
3 - 9/23-11/17*51/92 с подробным решением...
1 - [tex]\int\limits^x_0 {(x-t)f(t)} \, dt =x^4+x^3+x^2[/tex], найти f(0)...
1 - Роль афанасия лаврентьева в ,! желательно,коротко...
3 - Write questions with how long complete the answers with for or since....
3 - Укажите допустимые значения переменной в выражении только 2) и 4)...
3 - Не сложно 5. отметьте слова, в которых буква h не произносится: 1) what;...
3
Размер клетки в задаче не уточняется, поэтому сперва нужно определить, скольким условным единицам равна длина ее стороны.
Построим прямоугольный треугольник AOD, в котором AD является гипотенузой.
Длина AO равна 4 клеткам, длина OD равна 12 клеткам.
Пусть длина стороны клетки равна x условным единицам.
Тогда AO = 4x, OD = 12x.
По теореме Пифагора:
Это значит, что длина стороны клетки равна 0,5 условным единицам.
Формула площади ромба:
AC и BD — диагонали данного ромба, длина которых равна 24 и 8 клеткам соответственно.
AC = 24 ∙ 0,5 = 12;
BD = 8 ∙ 0,5 = 4.
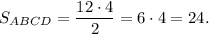
ответ: площадь ромба равна 24.