На доске написаны числа 1, 2, 3, 2018.за один ход разрешается стереть любые два числа и вместо них записать их разность.в результате многократного выполнен я таких действий на доске окажется записанным одно число. может ли оно быть нулем?
Другие вопросы по теме Математика
Популярные вопросы
- Расскажите о том, как распределяются заповедники по территории нашей...
3 - Определите показатели естественного прироста населения России в 2005...
3 - Определите величину естественного прироста в России в 1913 г., если на...
1 - Определите, на какие возрасты приходятся наибольшие потери населения,...
3 - Сравните возрастно-половые пирамиды России в 1897 и в 1997 гг. Какими...
3 - Назовите безлесные зоны нашей страны. Где они расположены? В чём их сходство...
3 - Составьте характеристику любой природной зоны по плану. Используйте при...
1 - Ознакомьтесь с прогнозами динамики численности населения. Какой из них...
2 - В чём причины неравномерного размещения населения по территории России?...
1 - Определите, о какой природной зоне идёт речь, если в ней растут: а) карликовая...
3
Сумма всех чисел на доске равна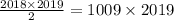 то есть нечетна. Покажем, что четность суммы не меняется, то есть последнее число должно оказаться нечетным.
то есть нечетна. Покажем, что четность суммы не меняется, то есть последнее число должно оказаться нечетным.
База: первым ходом стираются два числа. Так как их разность той же четности, что и их сумма, то четность суммы чисел не изменилась.
Переход: пусть после k ходов сумма нечетна. Покажем что следующим ходом мы не поменяем четность сумма. Но для этого достаточно применить рассуждения изложенные в базе. Значит через k+1 ход сумма чисел останется нечетной.
Так как 0 - число четное, а в итоге должно получиться нечетное число, то ответ на задачу отрицателен.
ответ: нет