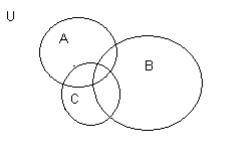
На диаграмме Венна для подмножеств А, В, С универсального множества U прямоугольник, изображающий U, разбивается на 8 перекрывающихся областей. Описать каждую их этих областей с операций объединения, пересечения и дополнения
Другие вопросы по теме Математика
Популярные вопросы
- Самостоятельно, найти x, по данному его логарифму ( 0, 0): А) log5 = 2...
3 - Напишите любой ответ! (и подпишитесь...
1 - Чем феодальная война второй четверти XV века отличается от феодальных...
2 - Местоимение – часть речи, которая… 1) обозначает предметы, признаки и...
2 - изолированный провод разрезали на три части и сплели в одну.Во сколько...
3 - написать упражнение , нужно большое )))...
3 - Здравствуйте решить 2 задачи по химии: а) определите массу сульфата натрия,...
3 - Вывод по эволюции оплодотворения...
1 - Вставьте необходимый предлог: to, on, for, from, about.1. Tim was absent………class...
1 - 9^(x) +1/2-28*3^(x-1)+1 =0...
1
1. Область A∩B∩C:
Эта область представляет собой пересечение всех трех множеств A, B и C. В данном случае, это значит, что эта область содержит только элементы, которые принадлежат одновременно множествам A, B и C.
2. Область A∩B∩C':
Эта область представляет собой пересечение множеств A, B и дополнения множества C. Это означает, что эта область содержит только элементы, которые принадлежат множествам A и B, но не принадлежат множеству C.
3. Область A∩B'∩C:
Эта область представляет собой пересечение множеств A и дополнения множества B, а также множества C. Это означает, что эта область содержит только элементы, которые принадлежат множествам A и C, но не принадлежат множеству B.
4. Область A∩B'∩C':
Эта область представляет собой пересечение множеств A и дополнения множеств B и C. Это значит, что эта область содержит только элементы, которые принадлежат множеству A, но не принадлежат ни множеству B, ни множеству C.
5. Область A'∩B∩C:
Эта область представляет собой пересечение множества A и дополнений множеств B и C. Это значит, что эта область содержит только элементы, которые принадлежат множествам B и C, но не принадлежат множеству A.
6. Область A'∩B∩C':
Эта область представляет собой пересечение дополнений множеств A, B и множества C. Это означает, что эта область содержит только элементы, которые принадлежат множеству C, но не принадлежат ни множеству A, ни множеству B.
7. Область A'∩B'∩C:
Эта область представляет собой пересечение дополнений множеств A, B и множества C. Это означает, что эта область содержит только элементы, которые принадлежат множеству C, но не принадлежат ни множеству A, ни множеству B.
8. Область A'∩B'∩C':
Эта область представляет собой пересечение дополнений всех трех множеств A, B и C. В данном случае, это значит, что эта область содержит только элементы, которые не принадлежат ни множеству A, ни множеству B, ни множеству C.
Надеюсь, что это объяснение помогло вам понять каждую область на диаграмме Венна и использование операций объединения, пересечения и дополнения. Если у вас есть еще вопросы, не стесняйтесь задавать их.