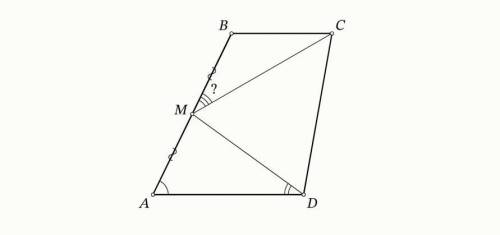
На боковой стороне AB трапеции ABCD (AD∥BC) отмечена середина M. Известно, что AD+BC=CD, ∠BAD=56∘, ∠MDA=47∘. Сколько градусов составляет угол BMC?​

Для решения этой задачи, нам понадобятся знания о свойствах трапеции и использование угловой суммы треугольника.

По свойству трапеции, сумма оснований равна сумме боковых сторон: AD + BC = CD. Данное условие нам поможет в дальнейших вычислениях.

Рассмотрим треугольник AMD. Мы знаем два его угла: ∠BAD = 56° и ∠MDA = 47°. Чтобы найти третий угол, воспользуемся угловой суммой треугольника: ∠AMD = 180° - (∠BAD + ∠MDA) = 180° - (56° + 47°) = 77°.

Таким образом, в треугольнике AMD, мы нашли все три угла: 56°, 47° и 77°. Продолжим решение задачи.

Обратим внимание на то, что M - середина боковой стороны AB трапеции ABCD. Поэтому, линия BC проходит через точку M и делит угол BMD на два равных угла (по свойству медианы). Обозначим угол BMC как α.

Таким образом, угол BMD составляет α градусов, а угол CMA также α градусов.

Мы знаем, что сумма углов в треугольнике BMD равна 180°: α + ∠BMD + ∠BDM = 180°. Отсюда, ∠BDM = 180° - α - α = 180° - 2α.

Аналогично, сумма углов в треугольнике CMA составляет 180°: α + ∠CMA + ∠CAM = 180°. Отсюда, ∠CAM = 180° - α - α = 180° - 2α.

Заметим, что треугольники BMD и CMA имеют общую боковую сторону BM и углы при этой стороне равны. То есть, треугольники BDM и CAM - подобные треугольники.

Из подобия треугольников, мы можем сравнить соответствующие углы. Так как ∠BDM = ∠CAM = 180° - 2α, то ∠DMB + ∠DCA = 180° - 2α.

Заметим, что углы ∠DMB и ∠DCA являются дополнительными углами к углам ∠BAD и ∠ADС соответственно. Поэтому, ∠DMB = 180° - ∠BAD и ∠DCA = 180° - ∠ADC.

Теперь мы можем записать равенство 180° - ∠BAD + 180° - ∠ADC = 180° - 2α.

Подставим известные значения ∠BAD = 56° и ∠ADC = 180° - ∠BAD = 180° - 56° = 124°.

Тогда получим 180° - 56° + 180° - 124° = 180° - 2α.

Упростим уравнение: 180° + 180° - 56° - 124° = 180° - 2α.

180° + 180° - 56° - 124° = 2 * 180° - 2α.

380° - 180° = 2α.
200° = 2α.

Теперь найдем α:
200° / 2 = α.
100° = α.

Таким образом, угол BMC составляет 100°.