N16 Найдите значение выражения (тема- прогрессии) 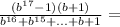
при b=-3
(У меня вышел ответ 8 , но в тестах указан 16, не могу найти ошибку()
всем, кто
Другие вопросы по теме Математика
Популярные вопросы
- Что такое комплексное изделие методы проектирование эскиз. всё это...
1 - В. д. герасимов тест для самопроверки номер 10 если 64 метра ситца...
1 - На доске написаны числа от одного до 299 раз в минуту какие-то два...
2 - Вданном ниже ряду слов найди слово в котором все согласные звуки...
3 - Какое вещество в данном состоянии не имеет собственной формы и занимает...
2 - Как будет по , ученица которая учится на тройки (троечница)? ответте...
3 - Для приготовления клубничного варенья требуется 5 частей ягод, 6...
1 - 9прочитай и отметь (м) правильный вариант.1 did susie play football...
3 - Втзначте індуктивність котушки, в якій під час зміни сили струму...
1 - 2000 дм3 =8 000 дм3 =3 000 см3 =90 000 дм3 =7 000 дм3 =...
3
b^n - 1 = (b - 1)(b^(n-1)+b*(n-2)++b^2 + b + 1)
b^17 - 1 = (b - 1)(b^16 + b^15 + + b^2+b+1)
(b^17 - 1)(b + 1)/(b^16 + b^15 + + b^2+b+1) = (b - 1)(b + 1) = b^2 - 1
b = -3
9 - 1 = 8
16 равно когда (b^17 - 1)(b - 1)/(b^16 + b^15 + + b^2+b+1) = (b - 1)(b - 1) = (b - 1)^2 ( (-3 - 1)^2 = 16)