N^n/(n+1)!
исследовать на сходимость ряда
Другие вопросы по теме Математика
Популярные вопросы
- 4. Катер проплыл 2,4 часа по течению и 4 часа такое же расстояние...
2 - ы или а,про 47 32 татарстан жэж клым...
3 - Выбери многочлены, записаные в стандартном виде. ...
3 - Лидер восстания в Присырдарьинском регионе . Впоследствии стал...
3 - 1008. задачу решить с уравнения. ...
2 - Позначте рядки речовин з іонним типом хімічного зв’язку: Na₂S;...
2 - Закончите СПП с сопоставительными отношениями 1. Чем дольше живёт...
2 - Ребят обоснуйте ответ почему я выбрала тему по проекту ,,правильное...
3 - При 25ºС растворимость соли Х равна 25г на 100 г воды. Какова формула...
3 - 2 - тапсырма Оқылым мәтіні негізінде мезгіл , мекен , мақсат мәнді...
1
По формуле Стирлинга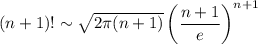
Тогда ряд расходится по признаку Коши
Вариант 2
Тогда ряд расходится по признаку Даламбера