1. Математика
  2. ∑∞,n=1 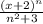. найдите радиус

∑∞,n=1 \frac{(x+2)^n}{n^2+3} . найдите радиус сходимости степенного ряда

kokosik23 kokosik23    3   19.07.2020 15:43    1

Ответы
37892 37892  15.10.2020 15:25

1

Пошаговое объяснение:

Воспользуемся признаком Даламбера

R=\lim\limits_{x\to \infty}|\frac{a_n}{a_{n+1}} |

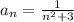
где a_n=\frac{1}{n^2+3}

Значит

R=\lim\limits_{x\to \infty}|\frac{(n+1)^2+3}{n^2+3} |=\lim\limits_{x\to \infty}|\frac{(n+1)^2+3}{n^2+3} |=\lim\limits_{x\to \infty}|\frac{n^2+2n+4}{n^2+3} |

Данный предел берется легко, достаточно разделить числитель и знаменатель на старшую степень

R=\lim\limits_{x\to \infty}|\frac{1+\frac{2}{n}+\frac{4}{n^2} }{1+\frac{3}{n^2} } |=1 .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Makoto2000 Makoto2000  28.05.2019 11:10
Как найти уравнение 75.880 : (n - 29.965) = 70...
kinzya kinzya  28.05.2019 11:10
Слагаемое 12 повторяется 4 раза. запиши такую сумму виде произведения...
chartenok88201ovseez chartenok88201ovseez  28.05.2019 11:10
1)пешеход за 4 ч км.с какой скоростью шел пешеход? записать ответ в виде смешанного числа. 2)длина прямоугольника =6 см,а площадь 21 см².найдите ширину прямоугольника....
кари345 кари345  28.05.2019 11:10
__о__б__в__а вова бросил мяч дальше,чем боря и олег, но ближе, чем артем. : нарисуй другой правильный вариант схемы....
ivanovartem02 ivanovartem02  28.05.2019 11:10
Запишите ответ в виде смешанного числа 1)пешеход за 4 часа км . с какой скоростью шёл пешеход 2) длина прямоугольника равна 6 см , площадь 21 см в квадрате . найдите...
Юлианана228 Юлианана228  28.05.2019 11:10
Сформулируйте правила личной безопасности и обоснуйте свои действия при смерче. ))...
Оно8885858855 Оно8885858855  28.05.2019 11:10
Решите уравнения 9(213-2х)=927 1344/(х+26)=32 384/(51-5х)=24...
ViktoriaTigra ViktoriaTigra  28.05.2019 11:10
Ц=375 кг 865 кг= .. =305 см 8 м 40 см см 732 см = дм 2 ч 30 мин. = мин...
элюсся5 элюсся5  28.05.2019 11:10
1.составь верные равенства используя числа 6,7,8,48,56....
татьянаивановна1 татьянаивановна1  28.05.2019 11:10
Составь верные равенства используя числа 6,7,8,48,56...

Популярные вопросы