(n-1)!/(n-3)!≤6
Определите количество целых решений ​

С учетом того, что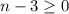 откуда 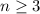ответом неравенства есть откуда целые решения это 3 и 4.

2

Пошаговое объяснение:

Для начала заметим, что аргумент факториала есть неотрицательное целое число, поэтому ОДЗ: n≥3, n ∈ Z.

Числитель дроби можно представить в виде: (n-1)! = (n-1)(n-2)·(n-3)!

Так как факториал не может обратиться в 0, то можно безболезненно сократить числитель и знаменатель на (n-3)!

(n-1)(n-2)≤6;

n²-3n+2≤6;

n²-3n-4≤0;

(n+1)(n-4)≤0;

Находим решение этого неравенства, например, методом интервалов: -1≤n≤4;

C учетом ОДЗ: 3≤n≤4.

Значит, целых решений всего два: 3 и 4