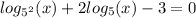 Можно ли решить этот пример заменой? Если да, то как?
Можно ли решить этот пример заменой? Если да, то как?
Другие вопросы по теме Математика
Популярные вопросы
- Начерти прямоугольник с длинами сторон 8 см и 4см. вычисли его периметр и площадь.заранье...
2 - 1)у собаки чёрная шерсть доминирует над коричневой , а коротконогость –над нормальной...
3 - Нужно произведение конан дойла горбун в сокращении...
2 - Нужно доказать тождество (a+b)²-2ab+a²-b²=a*2a...
3 - Что такое регенерация? для каких животных характерна?...
1 - Слово друг оно какое нарицательное или собствиное...
3 - Три серых котенка увидели мышку.они бросились за ней.мышка прыгнула в банку с мукой....
2 - Дейтерий может образоваться при поглощении водородом одного нейтрона. масса дейтерия...
1 - Как выглядел главный герой рассказа в. распутина уроки французского (мальчик). опишите...
1 - Если бы школьник купил 11 тетрадей, то у него осталось бы 8 рублей...
2
x = 5 и x = 1/125
Пошаговое объяснение:
Можно заменой и даже нужно!)
=========================
Сразу делаем замену: пускай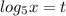 . Подставляем значение в уравнение:
. Подставляем значение в уравнение:
--------------------------------------------
Обратная замена:
Зная свойство логарифма (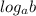 ↔
↔ 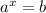 ) можем решить уравнения выше.
) можем решить уравнения выше.