Можно ли представить 1 в виде суммы 1000 дробей, числители которых равны 1, а знаменатели – нечетные числа?
Другие вопросы по теме Математика
Популярные вопросы
- Впарке посадили клёны и дубы, причём каждые 4 клёна приходится...
1 - Составьте уравнение реакции схема которой дана ниже: caco3--...
1 - Сколько железа и серной кислоты необходимо для получения 4,48л...
2 - Выделить целую часть дроби 360626231907767440 а) 19; б) 25; в)...
2 - Какие самые короткие сказки бажова?...
2 - Фонетический разбор слов ошибаетесь, гадостью...
2 - Анаграмма – приём, состоящий в перестановке букв или звуков определённого...
2 - Нужно провести классный час на тему умеем ли мы прощать ! заранее...
3 - Вцветнике распустилось 690 цветов.1/3 этого количества цветов...
2 - Какое число надо прибавить к числу 60 что бы получить разность...
2
Нет
Пошаговое объяснение:
Пусть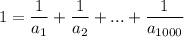
Приведём дроби к общему знаменателю: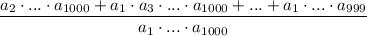
Получается, что в знаменателе находится произведение нечётных чисел, то есть нечётное число, а в числителе — чётное (1000) число нечётных произведений. Сумма чётного количества нечётных чисел есть число чётное.
Дробь равна единице только тогда, когда числитель равен знаменателю, но чётное число (числитель) не может быть равно нечётному (знаменатель). Противоречие.