Можно ли натуральные от 1 до 2020 разбить на 1010 пар так, чтобы разность чисел в первой паре была равна 1, во второй паре — 2, . . . , в последней паре — 1010?

нет

Пошаговое объяснение:

Предположим, что такое разбиение возможно и оно выполнено. Обозначим меньшие числа в парах буквами a с индексами:

Индекс совпадает с разностью чисел в паре, в которой состоит соответствующее число.

Тогда большее число в -той паре будет равно , а их (бОльших чисел) последовательность выглядеть так:

Вычислим сумму чисел от 1 до 2020 двумя . С одной стороны, ее можно найти как сумму первых 2020 элементов арифметической прогрессии с первым элементом 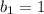и разностью :

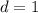С другой стороны, можно сложить суммы в парах чисел, используя введенные буквенные обозначения:

Сумму чисел во вторых скобках опять же найдем как сумму первых 1010 элементов арифметической прогрессии с первым элементом 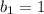и разностью :

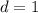Мы подошли к ключевому равенству: приравняем полученные разными путями суммы:

Отсюда

Однако сумма натуральных чисел не может быть дробной! Получили противоречие. А значит, разбиение, о котором идет речь в задаче, невозможно.