Может ли шестизначное число вида aaabbb быть квадратом натурального числа?( Цифры a и b необязательно различны)?

Нет

Пошаговое объяснение:

Пусть такое число существует.

Заметим:

Т.е. оно делится на 111 = 3*37 - не квадрат натурального числа. Т.к. исходное число - квадрат некого натурального числа, то оно должно делиться на 3²*37²=111². Т.к. , то должно выполняться условие

Оценка: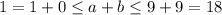 - ни одно число из данного промежутка, очевидно, не кратно 111. Противоречие.

А значит такого числа не существует.