Может ли дискриминант квадратного трехчлена с целыми коэффициентами быть равным 35? Чуть по подробнее )

Не  может  

Пошаговое объяснение:

Предположим противное  ,   предположим ,

что найдутся целые числа  а , b , с  :  b² - 4ac  = 35  ⇒ b² = 4ac +35  ( 1 )  

 ;   так  как  b² -  сумма  чётного  и нечётного  числа  , то  b² -  нечётно и

значит b  -  нечётно  ,  пусть  b = 2k+1  ⇒ b² = 4k² + 4k + 1   ;  подставим  в  

( 1)  :  4k² + 4k + 1  = 4ac +35  ⇒  4k² + 4k - 4ac = 34 ⇒ 2k² + 2k - 2ac = 17   ( 2)

равенство  ( 2 )  невозможно , так как левая часть кратна 2  , а правая

нет   и  значит  предположение  было  неверным ,

что  доказывает невозможность такого  дискриминанта  

Нет, не может

Пошаговое объяснение:

Дискриминант квадратного трехчлена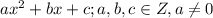 равен .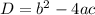

Возможны 2 ситуации

1)

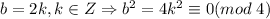
2)

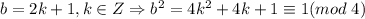
Слагаемое .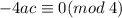

Значит, либо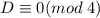 , либо .

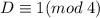Но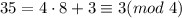 - противоречие.

Значит, дискриминант квадратного трехчлена с целыми коэффициентами не может быть равным 35.

Для записи использованы сравнения чисел по модулю